对输出数据进行划分

　　考虑下面的算法框架：
　　　　　　　

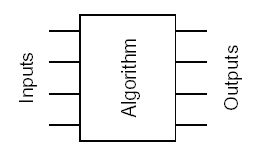
　　这个算法有一个输入集，经过处理后，得到一个输出集。如果输出集中的每个元素都是独立计算的，那么，对输出集的任何划分都会有一个对应的并行任务分解方案。这种分解的最大并行度等于输出集的规模。数据分解是一种很有效的发现并行性的方法。

　　下面考虑一个更为实际的例子。x，b是n维向量，A是一个n×n的矩阵，计算矩阵向量积如下：
　　　　　　　　　　　　　　b=Ax

　　显然，b是算法的输出，我们来看b的每个元素是如何得到的。b的每个元素可以用下面的公式的到：
　　　　　　　　　　　　　　
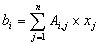
　　如下面的图所示：
　　　　　　　　　

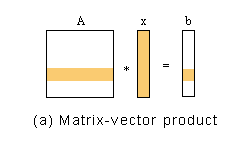
　　由于b的各元素的计算可以独立（并行）进行，我们可以将这个计算按照b的元素进行数据划分：n个处理器，每个处理器完成一个元素的计算。

　　现在考虑矩阵的乘法，描述如下：A，B，C都是n×n的矩阵的矩阵，完成下面的矩阵乘法：
　　　　　　　　　　　　　　C=A×B

　　这个算法通常被实现为下面的三重循环：
　　　　for (i=0; i<n; i++)
　　　　for (j=0; j<n; j++)
　　　　　for (c[i][j]=0.0, k=0； k<n； k++)
　　　　　　c[i][j] += a[i][k]*b[k][j];

　　它的计算示意图如下（C的每个元素的计算）：
　　　　　　　　　

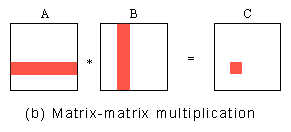
　　在这个算法中，C的每个元素是A的第i个行向量与B的第j个列向量的点积，因此，可以按照C的元素进行数据划分，并把计算每个C的元素的任务作为一个子任务。这种分解的最大并行度为n×n。