（8）超立方体 一个 -立方体由N=2ⁿ个结点组成，它们分布在n维上，每维有两个结点。0-立方体、1-立方体、2-立方体、3-立方体如下图所示。
　　

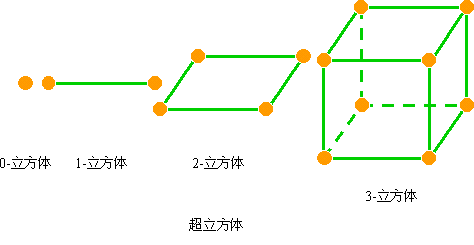
　　一般地，n-立方体可以通过两个(n-1)-立方体互连得到。例如，4-立方体可以用两个3-立方体互连得到。
　　　
　　一个n-立方体的结点度为n，网络直径也是n，对分宽度为N/2，对称。在80年代并行系统的研究开发工作中，超立方体是一种极为普遍采用的结构。Intel iPSC/1、iPSC/2和nCUBE机等并行机都采用了超立方体结构。许多并行算法也是针对超立方体结构设计的。这种结构的连接比较密集。它的一个特点是，许多其它结构诸如二叉树，网格和许多其它低维网络都能嵌入到超立方体中去。因此超立方体结构有很大的理论价值。但是超立方体结构也有很大的缺陷。它的结点度随维数线性增加，所以超立方体不是一种可扩展的结构。

　　由于超立方体缺乏可扩展性以及难于组成高维的超立方体，所以超立方体结构正逐渐被淘汰。例如，CM-5选用了胜过CM-2超立方体的胖树结构。Intel Paragon选用了较其前身超立方体更好的2维网格结构。