静态互连网络小结 下表列出了各种静态互连网络的特性。大多数网络的结点度都小于4，这是比较理想的。全连接网络和星形网络的结点度比较高。超立方体的结点度随着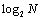值增大而增大，当N值很大时，其结点度也很高。

　　网络直径的变化范围很大。但是，随着硬件寻径技术的发展（例如虫蚀寻径技术的出现），源结点和目的结点之间的距离已经不是影响通信延迟的主要因素。在使用了类似于流水线操作的技术后（例如虫蚀寻径），任意两结点间的通信延迟几乎是相同的。链路数决定了实际使用的物理线路的数量，从而会影响网络的价格。网络的价格随结点度和链路数的增大而上升。等分宽度会影响网络的带宽。对称性会影响可扩展性和寻径效率。直径可以体现出两结点之间距离的上限，但是结点之间的平均距离可能能够更好地反映任意两结点之间的距离。

网络名称	网络规模	结点度	网络直径	对分宽度	是否对称	链路数
线性阵列	N个结点	2	N-1	1	否	N-1
环	N个结点	2	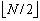(双向环） N-1（单向环）	2	是	N
全连接	N个结点	N-1	1		是	N(N-1)/2
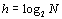
二叉树	N个结点, 树高	3	2(h-1)	1	否	N-1
星形	N个结点	N-1	2		否	N-1
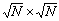
二维网格	个结点	4			否
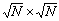
Illiac网	个结点	4			否	2N
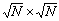
二维环绕网格	个结点	4			是	2N
超立方体	N=2n个结点	n	n	N/2	是	nN/2
带环立方体	N=n2n个结点	3		N/2n	是	3N/2
K元n-立方体	N=kn个结点	2n		2kn-1	是	nN