|
(4)均匀洗牌置换 均匀洗牌置换是把输入端分成数目相等的两半,前一半和后一半按原顺序相间排列的置换。这种置换很像洗扑克牌时将整副牌分成相等的两叠来洗,以达到一张隔一张的均匀状况,由此而得名。其表达式为
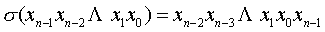 , ,
即均匀洗牌置换是将输入端地址的二进制编号循环左移一位的置换。它完成的变换如下图所示。

此外还可以定义子洗牌(subshuffle)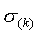 和超洗牌(supershuffle) 和超洗牌(supershuffle)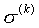 如下: 如下:
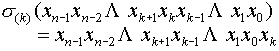 , ,
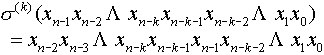 。 。
可以看出,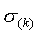 就是将输入端地址的二进制编号的低 就是将输入端地址的二进制编号的低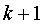 位循环左移1位,而 位循环左移1位,而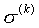 就是将输入端地址的二进制编号的高 就是将输入端地址的二进制编号的高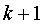 位循环左移1位。显然有 位循环左移1位。显然有
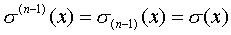
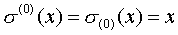
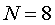 , ,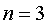 时 时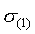 与 与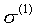 的变换情况如下图所示。 的变换情况如下图所示。
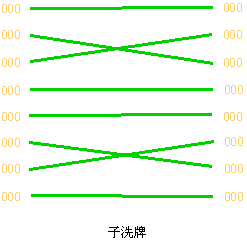
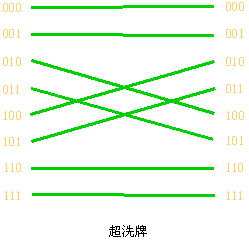
从上图可以看出,子洗牌是将所有地址分成若干子组,对每个子组进行均匀洗牌变换。超洗牌虽然仍是对整组地址进行均匀洗牌变换,但是增加了变换的移位量。
逆均匀洗牌是均匀洗牌的逆函数,即将输入端二进制地址循环右移1位。其函数表达式为
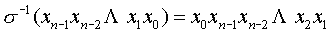
它所完成的变换如下图所示。与均匀洗牌相比,它们的输入端和输出端恰好互换了位置。

均匀洗牌和逆均匀洗牌是两种十分有用的互连函数,以它们与交换置换组合起来可构成Omega网络(即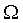 网络)与逆Omega网络( 网络)与逆Omega网络(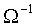 网络)。
函数在实现多项式求值、矩阵转置和FFT(快速傅立叶变换)等并行运算以及并行排序等方面都有广泛的应用。 网络)。
函数在实现多项式求值、矩阵转置和FFT(快速傅立叶变换)等并行运算以及并行排序等方面都有广泛的应用。
|