|
5.感知机
感知机是在1957年由Rosenbllatt提出的,它是一种由单层神经元组成的神经网络。以两类情况(A和B)的分类问题为例,设输入为n维样本xo,x1,…xn,感知机如图
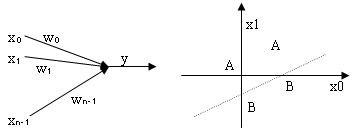 |
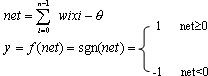
分类的判别准则为:
y=1→A类
y=-1→B类
分类器相当于在n维样本空间建立一个超平面
作为决策面,二维样本的情况如图所示,若输入样本落入超平面正侧,即使上述左侧为正,则判决为A类;若输入样本落入超平面负侧,即使上述左侧为负,则判决为B类。为简单起见,可定义广义输入样本X和广义权值为n+1维向量:
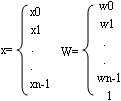
感知机可描述为
net=WTX
y=f(net)=sgn(net)
其中,T表示矩阵的转置。分类器的超平面方程变为线性齐次方程:
WTX=0
此时,决策面变成n+1维空间的一个通过原点的超平面。
感知机的学习问题归结为如下问题:
已知:一组有类别标志的广义样本集X={X1,X2,…Xn}
准则函数J(W)
求解:使准则函数J(W)最优的极值解
不同的准则函数和最优化酸法可得到不同的学习算法。这里我们取准则函数为
其中,dk和yk分别为第k个样本对应的正确输出和实际输出。显然,上式仅针对错误划分的样本求和。错误划分有两种情况:
(1) A类误判为B类,即dk=1,yk=-1。此时有
因此
(2) B类误判为A类,即dk=-1,yk=1。此时有
因此
在两种情况下,Jp(W)中求和号内各项均为非负,且误分越少,准则函数Jp(W)就越小,Jp(W)为0时全部正确分类。最优化酸法采用剃度下降法,样本集合和线性可分时,这个算法是收敛的。
综上所述,感知机的学习算法如下:
(1) 初始化
设t=1,及广义权值向量 W1={wo,w1,…,wn-1,-θ}T的各分量为小的随机数。
(2) 提供新的输入和理想输出
新的输入表示为广义向量Xt={xo,x1,…xn-1,-1 }T,理想输出为d
(3) 计算实际输出
yt=sgn(WtTXt)
(4) 调整权值
Wt+1=Wt+ t(dt-yt)Xt
其中ηt≤1
(5) 若全部样本都已正确分类或迭代达到预定次数,则结束;否则,t→t+1,转(2)
感知机只能解决线性可分的问题,对简单的异或问题也无能为力。可以证明,在输入层和输出层之间再加一层隐单元,即可解决异或问题。若假两层隐单元,即可对任意复杂的分布进行分类。需要解决的是多层网络的学习问题。