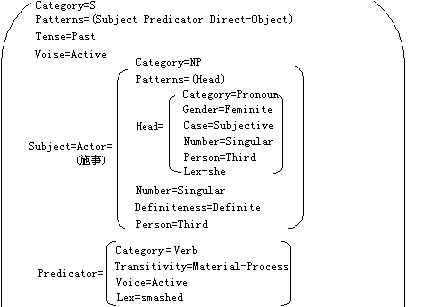
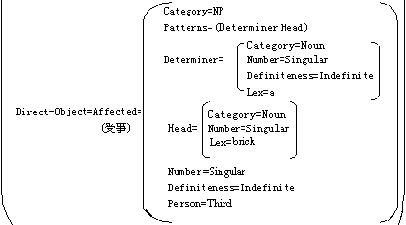
|
合一(unification)有点象集合论中的并(union)。并集所取的是各个集合里所有不同元素组成的集合，如
{A,B}∪{C,B}={A,B,C}
值得注意的是，在集合运算中总是把集合中的元素看作是不可分解的原子。即使其中的元素是有序对，如(fi，vi)表示特征fi的值为vi，求并集时它们仍被当作不可再分的个体来看待；而不考虑它们的内部结构。假设
α＝{(f1，v1)，(f2，v2)}
β＝{(f1，v1')}
而且v1≠v1'，表示集合α和β所表达的信息是互相抵触的，因为特征f1不允许同时拥有两个不相同的值。但是它们的并集仍为：
γ=α∪β={(f1，v1)，(f1，v1')，(f2，v2)}
不过从信息组合与传递的观点来看，并集Y所表达的信息是毫无意义的。
从谓词演算中借用过来的"合一"概念，在这一点上不同于并。因为根据定义，当两个集合所表达的信息发生冲突时，其合一结果为空集φ。表示合一失败。如果用符号"
"表示合一，则上例中α
β=φ
 |
定义 |
| 合一 1.若a与b均为原子，则 a
b＝a，当且仅当a＝b；否则a
b＝φ。2.若α与β均为复杂特征集，则 (1) 若a(f)＝v，而β(f)的值未定义， 则f＝v属于α β；(2) 若β(f)＝v.而α(f)的值未定义， 则f＝v属于α β；(3) 若α(f)＝v，β(f)＝v'， 则f＝(v
v')属于αβ；否则α β＝φ |
从以上定义的2(3)来看，这是一个递归定义。由于f的值v和v'本身又可以是复杂特征集，因此仅当v和v'可以合一时α和β才能合一。
如果把自然语言看作是-个信息传递系统，并且承认自然语言的合成性(compositionality)假设，即无论是句法成分还是语义成分都是按由小到大的方式逐步组合出来的，那么采用合一作为句法和语义分析的基本运算是非常理想的。因为：
(1)一个句子或其他语法单位所承载的信息总是分布在它的各个成分中。所以每个成分承载的是局部信息。
(2)通过合-运算把小成分组合成更大成分的过程中，每个小成分所承载的信息也同时被传递和累加成为更大成分所承载的信息。在这个过程中信息只增不减。
(3)由于句法和语义都以合一为基本运算，不仅某些句法结构的歧义可以通过语义手段来排除，而且在句子的句法结构和语义表示之间找到了-种更自然的衔接方式。
(4)由定义可知，合一运算是无序的，即不论合-从哪个方向开始，也不管其运算的先后次序如何，合一结果都相同。合-的无序性不仅适宜于并行处理，而且使我们有可能自由地选择分析算法和语法理论。
FD1：
