|
让我们作为一个例子来考虑被动转换规则。这条规则的结构索引是:
NP AUX V NP by pass
它的结构改变是:
4 2 be十en十3 0 5 1
把它应用到图9.6的树上,它产生用虚线表示的适当分析,然后用上述转换产生图9.7所示的树。
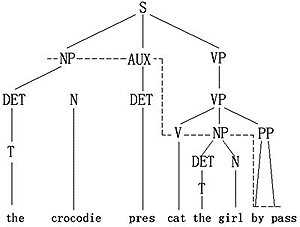 图9.6 对一棵深层结构树的一个截断 |
|
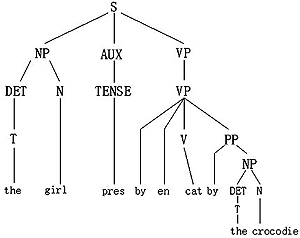 图9.7 对图9.6应用被动转换规则后所产生的树 |
除了结构索引和结构改变这两个主要部分以外,某些转换规则还可能有一个同一性条,即为了应用一条转换规则,要求被结构索引的两个元素所匹配的子树是相同的。
使基础部件成为递归的规则
COMP→#S#
在转换规则中也发挥了一种特别的作用。如果图9.8所示的结构出现在句法树中,我们把被这个S所支配的树叫做一个成分句(constituent sentence),或嵌入句;而把图9.8 COMP→#S#的树状结构被COMP上面的那个S所支配的树叫做主句(matrix sentence)句法树。
转换有两类:一元的和二元(或嵌入)的。在一个一元的转换中,结构索引不含有符号#。在一个二元的转换中,结构索引的形式为:
a#b#c
其中a,b,c是不包含并的符号串。二元转换删除这些边界标记(如果边界标记#是结构索引中的第i个和第j个分量,则无论是i还是j都不会在结构改变的任何地方出现),从而把一个成分句同它的主句组合起来。举例来说,一个二元转换将把"I believe COMP"的树同(在COMP底下)"Mary likes cheese"的树组合在一起形成"I believe Mary likes cheese."
转换还可以被分成可选的(optional)和强制的(obligatory)两大类。就象用一部上下文无关语法来进行句子生成一样,把转换应用于一个基础结构也许可以看作是一个非确定性过程。从一个单一的深层结构出发,根据所作的选择可以获得一个或几个表层结构。转换规则暂时被想象成按某种固定顺序来描述的。对于一条转换规则来说,如果不存在一个适当分析,这条规则就被跳过。如果存在几种适当分析,其中的一条规则就被选用。如果这条规则是强制的,它立即被应用;如果它是可选的,那么就要在用和不用之间作出一种选择。
一元的和二元的转换规则是分别排序的。转换过程总是通过选出一棵不再包含任何其他嵌入句的嵌入句树作为开始。对这棵树顺序地应用一元转换规则;结构索引只对这棵嵌入树而不是完整的树进行匹配。然后把二元转换规则应用到这棵树和它的主句树上来,其中的一条规则将对这棵树进行转换,删除嵌入句的边界#…#(如果没有一条规则能应用,那么最终的表层结构中会包含若干个#,这样的结构将被拒绝)。接下去选择另一个最深的嵌入句,重复这个过程直至不再有剩下的嵌入句为止。这时再利用一元转换规则来处理那棵完整的树,并完成整个生成过程。当然,如果基础结构中不包含嵌入句,那么生成过程只需一步就够了。