|
9.4.2 上下文无关语法的分析算法
用一部短语结构法来对一个句子进行句法分析，意味着寻找一个从起始符到该句子的推导－－一个产生式序。这个推导通常表现为一棵句法树歧义的（存在几种推导）好么将有几棵句法树。
举例来说，如果我们的语法是：
<S>∷＝<NP><VP>
<NP>∷＝<*N>|<*PRO>
<VP>∷＝<*TV>|<*TV><NP>
那么句子：
"I like cheese." (我喜欢奶酪。)
(其中"I"是PRO，"like"是TV，"cheese"是N)的最左推导是：
S
NP
VPPRO
VPPRO
TV NPPRO
TV N对应的句法树如图9.2(b)所示。
句法分析器可分为自顶向下(top-down)和自底向上(bottom-up)两大类。一个自顶向下的句法分析器从树顶的根结点开始建立句法树；用推导的顺序来说，它从起始符开始向着这个句子来进行推导。相反，一个自底向上的句法分析器从树底部的叶结点(即词或词类)开始建立句法树；用推导的顺序来说，它从句子开始，应用归约(产生式被倒过来用)直至到达起始符。
 |
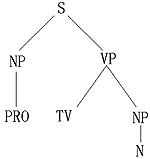 图9.2(b) 句子"I like cheese"的句法树 |
句法分析器还可以分类为回溯算法和并行算法。回溯算法每次只尝试一种推导，当这种推导失败时便"返回"以试验另一种推导。并行算法实际上同时进行所有的推导。
1.自顶向下的回溯算法
在各种上下文无关的句法分析器中，最普通的是采用自顶向下回溯算法的分析器。它逐个地枚举推导直至找到一个能生成输入句子的推导。我们可以把它作为一种串行算法描写如下。
这个算法对如下形式的一个推导进行运算：
S
z1z2…zn一开始这个推导仅包含起始符S。假设左侧符号为A的产生式的排列顺序是：PA.1，PA.2，…
(1)令zn中最左端的非终结符为B，用PB.1来展开B(于是给推导增添一个元素，令n＝n+1)。
(2)令zn中最左端的非终结符所处的位置为i(如果zn没有非终结符，则令i＝[zn的长度]+1)；如果Zn的前i一1个(终结)符号同输入句子的前i-1个词相匹配，则转至(3)，否则转至(5)。
(3)如果Zn仍含有非终结符，转至(1)。
(4)如果zn同被分析的句子匹配，把当前推导作为该句子的一个推导记下。
(5)令最近应用于推导的产生式为PB.i；如果存在产生式PBi+1，那么用PB.i+1的应用结果去取代推导的上一步，并转至(2)，否则转至(6)。
(6)从推导中删除最近的那条产生式，令n＝n-1；如果不再有产生式留下(推导只含有起始符)，则退出，否则转向(5)。
这个算法可以处理任何不具有左递归
的语法。对于左递归语法，必须附加某些测试以避免陷入无限循环。对于上面那部只有三条规则的语法和句子"I like cheese"，应用上述算法推导将增长和收缩如下：
S
S
NP
VPS
NP
VPN
VPS
NP
VPPRO
VPS
NP
VPPRO
VPPRO
TVS
NP
VPPRO
VPPRO
TV NPS
NP
VPPRO
VPPRO
TV NPPRO
TV N(把推导作为一个分析记录下来)
S
NP
VPPRO
VPPRO
TV NPPRO
TV PROS
NP
VPPRO
VPPRO
TV NPS
NP
VPPRO
VPS
NP
VPS
这个过程也可以用一系列自顶向下生成的树来表示(见图9.3)。
|
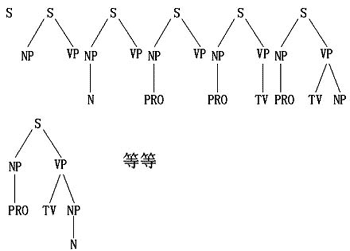 图9.3 句子"I like cheese"的推导过程 |