|
9.3.2 上下文无关语法(2型语法)
在乔姆斯基体系中生成能力略强于正则语法的是上下文无关语法。在一部上下文无关语法中，每一条规则都采用如下的形式
A→x
其中，A∈N，x∈V*，即每条产生式的左侧必须是一个单独的非终结符。在这种形式体系中，规则被应用时不依赖于符号A所处的上下文，因此称为上下文无关语法。在9.2.1中给出的第一部短语结构语法
S→aSc
S→b
就是上下文无关语法的一例。如果我们稍微改变一下规则中的符号，令
S→(S)
S→x
便可以生成前面提到的成对括号表达式：
x，(x)，((x))，(((x)))，((((x)))),…
上下文无关语法正是以这种方式解决了正则语法所不可能解决的嵌套结构。
上下文无关语法被广泛应用于程序设计语言和自然语言的描写中；在专业文献中，我们时常看到用所谓巴科斯-诺尔范式(BNF)来表达上下文无关语法，它同迄今我们用来表示短语结构语法的标记方法略有不同。在BNF中，我们用尖括号来标明非终结符，用符号" "代替"→"。此外，如果有两条或更多的产生式具有相同的左侧，它们可以作为一条单独的BNF定义被聚集在一起，并用符号"|"分隔。因此我们那两条用来生成对括号表达式的产生式规则可以用一条单独的BNF定义来表示：
<S>∷＝(<S>)＝|x
在符号"∷＝"右面用"|"隔开的两个串叫做定义的选择项，所以上式中S的定义有两个选择项。
除了表达上下文无关语法以外，我们还时常需要表达句子的推导(derivations)。推导显示出一个特定句子是怎样根据语法规则来生成的。我们可以把推导表示为产生式应用的一个线性序。
举例来说，如果有语法
<SENTENCE>∷＝<SUBJECT><VERBPHRASE> (1)
<SUBJECT>∷＝John|Mary (2)
<VERBPHRASE>∷＝<VERB><OBJECT> (3)
<VERB>∷＝eats|drinks (4)
<OBJECT>∷＝wine|cheese (5)
我们可以把句子"Mary eats cheese"的推导表示如下：
<SENTENCE>
<SUBJECT><VERBPHRASE>
(1)Mary<VBRBPHRASE>
(2)Mary<VERB><OBJECT>
(3)Mary
eats<OBJECT> (4)Mary
eats cheese (5)但是，如果我们把这种推导表示为一棵句法树(见图9.2(a))，也许会更清楚一些。
 |
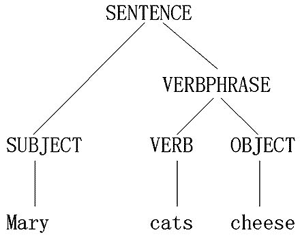
图9.2(a) 句子"Mary eats cheese"的句法分析树 |
起始符总是出现在树的根上，终结符则出现在树的叶子上。由于图上并未指明符号被重写的顺序，所以严格地讲这棵树所对应的推导不是唯一的。例如，下面的推导同样可以和这棵树对应：
<SENTENCE>
<SUBJECT><VERBPHRASE>
(1)<SUBJECT><VERB>(OBJECT)
(3)<SUBJECT>eats<OBJECT>
(4)Mary
eats<OBJECT> (2)Mary
eats cheese (5)在确定一个句子的推导时，通常对这些顺序上的变化不感兴趣，所以要规定某种标准顺序，并且只生成符合这种顺序的推导。
所谓最左推导(leftmost derivation)便是这类标准顺序中的一种，在这种规定下在每一步中总是重写最左边的那个非终结符。对于句子"Mary eats cheese"所给出的第一个推导就是这种最左推导的一个例子。每一棵句法分析树都严格地对应于一个最左推导。
一般来讲，这样一类语法总是比那些较强的语法更容易处理。
但是在某些情况下确实需要对一条产生式可以被应用的上下文加以限制，这就是乔姆斯基体系中的下一类语法,即上下文有关语法。