|
9.3 乔姆斯基体系
9.3.1 正则语法(3型语法)
正则语法有两种形式:左线性语法(left-linear grammars)和右线性语法(right-linear grammars)。在一部左线性语法中,所有规则必须采用如下形式:
A→Bt
或
A→t
其中A,B∈N,t∈T,即A,B都是单独的非终结符,t是单独的终结符。而在一部右线性语法中,所有规则必须如下书写:
A→tB
或
A→t
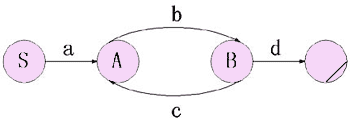
举例来说,下面是一部右线性语法:
S→aA
A→bB
B→cA
B→d
其中,S,A,B∈N,a,b,c,d∈T,S为起始符。这部语法所生成的句子由"ab"开头,后跟以零个或多"cb",最后用一个"d"结尾。
对于一部正则语法,我们总能用象图9.1那样的有限状态转移图(Finite-State Transition Diagram,简称FSTD)来表示。图上每个带标记的结点对应于一个非终结符,另外有一个特殊结点叫做最后结点,用带斜线的圆表示。每个结点对应于生成中的一个状态。对于每条形如
A→tB
的规则,便从结点A到结点B画一条弧;并在弧上标注终结符t。对每条形如
A→t
|
|
的规则,则从结点A到最后结点画一条弧,并在弧上标注终结符t。
为了生成被一部正则语法所定义的语言中的一个句子,只在与其对应的有限状态转移图上,从起始结点开始,沿着任何一条弧从当前结点转移到下一个新结点,并记下该弧上标注的符号。当到达最后结点时,我们所记下的符号串便是这种语言的一个句子。换言之,在状态转移图上每一条从起始结点到最后结点的路径都对应于被这部语法所生成的语言中的一个句子。
因此,正则语法又叫做有限状态语法。"有限状态"指的是图中结点的数量是有限的。当我们处于一个句子的生成过程中,为了正确地结束这个句子,需要知道的唯一信息就是当前所处的状态(结点),而无需了解已经生成的那部分句子的其他任何情况。
正则语法之所以引人注目是因为有限状态网络提供了一种可用来生成和分析语言的简单机制。遗憾的是,许多有趣的语言不能由正则语法来生成。一个简单的例子是字母"x"两边围以任意数量的成对括号:
x,(x),((x)),(((x))),((((x)))),…
为了生成这种语言的一个句子,当生成到"x"时我们必须知道前面已经生成了多少个"(",以便能生成同样数量的")"。所以这种语言是不能由正则语法生成的。
在英语中也有这种类似的嵌套构造。假设S1,S2,…是英语句子,我们可以利用如下的构造
if S1 then S2
either S1 or S2
the man who said that S1is arriving tomorrow
来把它们组合成更大的句子。后者又可以以嵌套的方式形成甚至更大的句子,如
if the man who said that either S1 or S2 is arriving tomorrow then S3
因此一部用来生成英语句子的程序必须记住,当它经过S1时前面曾经生成过什么样的构造,以便为同"either"匹配而生成"or",为同"if",匹配而生成"then"。这个问题同要生成成对的括号表达式类似。这样一类的构造说明,一个有限状态转移网络(正则语法),就如同不适宜用来描写括号表达式一样,也不适宜用来描写象英语那样的自然语言。