|
3.AM的初始知识库
图 7.15表示AM初始知识库中部分概念的层次。除了图中表示的以外,在STRUCTURE概念以下是许多重要的数据结构,如SETS,BAGS,ORDERED SETS,LISTS和ORDERED PAIRS。在ACTIVITY概念以下有许多运算,如SET-UNION,SETINTERSECT,SET-DIFFERENCE,SET-DELETION等。还有几个生成概念的操作,如PARALLEL-JOIN,RESTRICT,PROJECTION等。也有对于BAGS,ORDERED SETS,LISTS的操作。在PREDICATES下面是常值谓词TRUE和FALSE,概念EQUALITY。在各概念上共附有242条启发式规则。
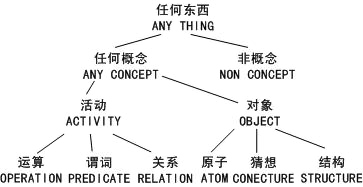 图7.15 部分初始概念的层次 |
4.AM的结果
AM开始运行时,它只有少量集合论概念。它发现了大多数明显的集合论关系,例如De Morgan定律。由于AM不了解抽象代数,所以它的陈述和证明比较含糊。AM没有引出无限集合的描述,但是它猜想"集合不能是自身的成员",还提供了构成新集合的连锁过程,这是把集合放入自身得到新集合。
此后,AM认为值得对"相等"概念进行一般化,从而发现了"同样大小"。由此发现了自然数,并定义出大部分算术运算。它模仿并集发现了加法,又用三种方式发现了乘法(作为重复的加法,作为类似笛卡儿积的运算,使用两个集合并集的幂集的基)。它还发现了四次乘幂和四次方根。
它发现了许多有意义的数字运算和数字种类。如奇数、偶数、二倍、二等分、整数次方根等,它分离出没有平方根的数的集合。它没有发现关系,没有提出"闭"的概念。它得到了乘法交换律和结合律,并以数字的包为乘法的参数。它把乘法的逆操作定义为"大于1 的数字的包,其乘积是X"。这正是X因式分解的概念。它把素数说成最小可分解的数,并认为最大可分解的数没有意义。它以奇怪的方式发现了素数,这是通过限制素数加法的论域和值域(即在素数中p + q=r的解)。AM猜测出算术基本定理(因子分解成素数的唯一性)和哥德巴赫猜想(每个大于2的偶数都是两个素数之和)。AM没有提出指数符号,也没有提出余数、大于、最大公分母等概念。这妨碍了数论的发展。
在补充一些初始几何概念后,它提出一些新的定义,如平行、相等测量、相似、全等、位移和旋转等,以及许多未命名的东西(如有一个公共角的两个三角形)。由于缺乏几何模型,它提出了许多不合理的几何猜想。
5.结论
AM的结果说明,一个不大的启发式规则集就可以指导很有意义的发现过程。例如,使用同样的启发式规则,把分解数字用于乘法逆就得到唯一因式分解,把分解数字用于加法逆就得到哥德巴赫猜想。
AM的一个缺点是无法改进现有的启发式规则。因此,它运行时间越长,定义的新概念就越多,启发式方法的效果就越差。Lenat(1980)提出发展启发式规则的方法。
另一个缺点是这些方法不适于其它领域。初等数学中概念的密度很高,每步的局部概念都利于构成复杂概念。但在很多领域中,难以评价局部解的关心程度。例如在下棋中难以评价一步棋的优劣。