第七章 其它学习方法

　　(3)分类的动态修改
　　上面得到的聚类把所有已观察的事件划分成不相交的几类。但是聚类中各复合的并集不一定覆盖整个事件空间。因此若考虑在这个并集以外的未观察事件，这些事件没有分到任一类型。为了考虑一个新的事件，应该自动调整分类。这由不相交化过程实现0过程如下。把当前聚类中的复合作为核心复合，把新事件作为m-list的元素。由不相交化过程把该事件放入它的最佳宿主复合中。于是，初始复合就成为它和该事件的合并(refunion)。
　　(4)聚类模块的例子
　　 共有10个对象。每个对象用4个变量描述，即X1,X2,X3和X4。变量论域都是
　　　DOM(Xi)＝ 0,1,2 ，i＝1,3,4
变量X1和X3是线性的，X2是结构的，X4是名称的。X2论域的一般化体系如图 7.11所示。

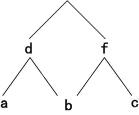图7.11 X2论域的一般化体系

对象的描述如图 7.12所示。

事件 X1 X2 X3 X4 事件 X1 X2 X3 X4 e1 e2 e3 e4 d5 0　a　0　1 0　b　0　0 0　c　1　2 1　a　0　2 1　c　1　1 e6 e7 e8 e9 c10 2　a　1　0 2　b　0　1 2　c　0　0 2　b　0　1 2　c　2　2 变量类型 L　S　L　N 变量类型 L　S　L　N （L：线性，N：名称，S：结构） 图7.12 对象的描述

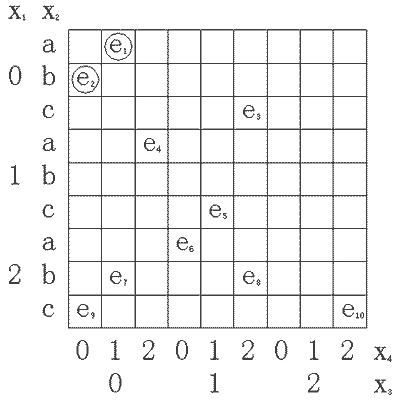图7.13 事件的几何表示

　　第一次迭代
　　步骤1：对K＝2，选2个已观察事件为根。可以任选，也可以选句法距离最大的事件(这时算法收敛较快)。为了选择这种突出的事件，可以用ESEL程序(Michalski和Larson，1978)。本例选两个差的初始根，选两个接近的事件e1和e2。
　　步骤2：由限制星过程(boundstar过程)产生限制简化星RG(e1|{e2}，m)和 RG(e2|{e1}，m)，并取m＝5，于是有
　　s
结构变量X2的选择器中的"b∨c"可以换成更一般的值f。这是攀登一般化体系规则。对线性变量X3,可以用闭合区间规则。于是星就成为
　　
　　步骤3：从每个星中选一个复合，进行适当修改，使2个复合组成的集合是E的不相交覆盖，而且是在所有可能的这种覆盖中按LEF最优或次最优的。因为它的总稀疏性，所以要考虑下列四种组合，从中选出覆盖(a)。四种组合如图 7.14所示。

稀疏性　简单性 (a)复合1：[X2=a][X3≤1] 　 复合2：[X2=f] 　　　　15　　　　2 　　　　47　　　　1 　　　　62　　　　3 (b)复合1：[X1=1∨2] 　 复合2：[X2=f] 这些覆盖不是不相交的，对这些覆盖用不相交化过程，但每种情况得到的聚类的稀疏性都≥62，而且简单性是3。 (c)复合1：[X2=a][X3≤1] 　 复合2：[X4=0∨2] (d)复合1：[X4=1∨2] 　 复合2：[X4=0∨2] 图7.14 四种组合

　　步骤4：检查结束条件。结束条件的参数b＝2，p＝2。这次迭代是第一次b迭代。
　　步骤5：确定两个新的根。这些根是覆盖(a)的已观察事件中的中心事件。复合[X2=a][X3≤1]覆盖集合{e1,e4,e6}，复合[X2=f]覆盖集合{e2,e3,e5,e7,e8,e9,e10}。注意X2的根f是b和c的一般化。由句法距离分别确定两个集合的中心事件e4和e8。这是新根。