|
(2)CLUSTER/2使用的路径队列排序搜索
上述由根确定聚类的方法很简单，但对实际问题的效率太低。这是因为一个星可能包含很多复合。在有n个变量和K个根时，一个星可能包含nK-1个复合。(因为计算一个完全的星要用到K-1个初步星，每个初步星至多有n个复合)。例如n＝30和K＝3，则有nK-1＝900个复合。于是穷举搜索树中，每个节点有900个枝，树有9003个叶节点。可以用吸收律消除一些多余的复合，但是星仍然太大。对上述全搜索方案的改进是用启发式方法简化搜索。
下面利用已知概念提出新的方法，它组合了下列四种方法，得到路径队列排序(PRO)搜索。
方法一：限制星(boundstar过程)
在一个星中复合的数目限定在固定的数目m，这确保树上每个节点至多有m个枝。限制星不是从初始星中任取m个复合，而是取m个最优复合。在减稀疏性过程中的第二步构造星时，首先对复合进行简化，然后按LEF准则下降的次序对复合排序。只保留前m个复合。于是最后得到的星只有m个复合。这个星称为限制简化星，并写成RG(e|E0，m)。利用限制星可以大大提高效率，得不能确保得到最优的聚类。这对搜索影响不大，因为每次迭代得到的聚类只影响下次迭代的根。所以其最优性并不重要。
方法二：动态地产生星
因为必须对以前选定的复合来评价复合，所以限制星对树的每个节点是不同的。只有必须扩展路径上正在研究的一个节点时，才产生星。这称为"迟钝"策略。
方法三：按路径队列次序搜索
在限制星中的复合是按LEF下降次序排列的。在树上，到最优复合的枝赋给枝标号0，到下一个最优复合的枝赋给枝标号1，依此类推直到枝标号m-1。由根到叶的一条路径的标号是沿路径各枝标号之和。由根到叶的一条路径表示一个可能的聚类。对各路径按标号大小次序排列。第一次研究标号为0的路径，它只包含每个星的最佳复合。其次考虑标号为1的路径，这种路径有K条。
在搜索中，当路径标号增加时，应该考虑搜索结束条件，结束条件有两个参数：搜索基础b和搜索试探p。搜索基础的路径数b是必须扩展和评价的。此后才考虑搜索试探的附加路径数p。对每条路径都要使用不相交化过程。当新聚类优于以前的聚类时，就保存它，并研究另一个搜索试探附加路径。
方法四：削减搜索树
星的限制m随着路径标号增加而减少。这使搜索范围更合理。
CLUSTER/2组合了上述四种方法，它的搜索树的示意图如图 7.10所示。m的最大值为3。扩展根的过程是构成限制简化星RG(根1|其它根，3)，它的复合是
11,12和13。(按LEF下降次序排列。)表示这些复合的三个枝分别赋给枝标号0，1和2。其次扩展连到枝0的节点，这生成星RG(根2|其它根，3)，产生复合
21,22和23。对应这些复合的枝赋给标号0，1和2。首先考虑路径0-1。它有最小路径标号0。用不相交化过程处理相应聚类
11,21，并把结果作为当时的最佳聚类保存下来。然后考虑路径0-1。用不相交化过程处理相应聚类
11,22，并由LEF评价。如果它优于以前的聚类，就由它代替原有聚类。此后研究路径1-0，这是第二条路径标号为1的路径。为此要产生星，RG(根2|其它根，2)。这个星包括复合
21'和22'。对路径1一0的聚类
12，21'进行不相交化和评价处理。如果结束条件是b＝2和p＝2，且评价得分如图。则树搜索在研究第四条路径0-2后结束。评分22的路径0-1是找到的最佳聚类。b＝2要求必须考虑路径0-0和0-1。而p＝2表示考虑完路径1-0和0-2这两条未改善的路径后过程结束。
 |
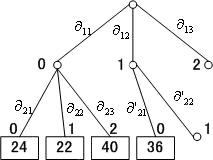 j表示星i的复合j ①,②,…表示扩展节点次序0,1,…表示枝标号 24,22,…表示路径的聚类评分 图7.10路径队列排序搜索树 |