|
(9)覆盖
令E1和E2是不相交的事件集合，E1对E2的覆盖写作COV(E1|E2)，它是s-complex的一个集合{
j}j∈J,使得对任一个e∈E1都存在一个j(j∈J)，使得j覆盖e，而且任一个j(j∈J)都不覆盖E2中任一个事件。(其中j覆盖e表示e满足j的所有选择器。)上述条件可以等价于
若把覆盖中的各复合
j都表示为l-complex，则覆盖可以表示为这些复合的析取
。若一个覆盖中所有的s-complex互不相交，则称为不相交的覆盖。如果E1是被聚类的集合，E2＝
，则不相交的覆盖COV(E1|)可以简写为COV(E1)，它表示事件的不相交聚类。下列算法就是产生事件的不相交聚类，这是通过反复构造特殊的覆盖，这些覆盖称为星。
(10)星(star)
设e
E0，事件e对于事件集合E0的星写作G(e|E0)，这是一些最一般的复合，使之覆盖e但不覆盖E0中任一事件。所谓"最一般的"是指不存在同样的复合G'，使G(e|E0)
G'。图
7.8是星G(e|E0)的例子。事件是在两个线性变量生成的二维空间中的点。E0是由黑点组成的集合。星G(e|E0)包括复合1,2和3。星中不包括'3，因为'33。
 |
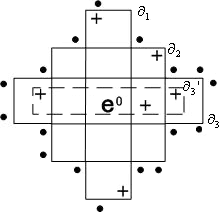 图7.8 星G（e|E0） |
下列算法中将对理论上的星进行两种修改。一种是使星中复合的稀疏性减小。这是由减稀疏性过程(redustar过程)实现。另一种是限制这个星，这是根据上下文有关准则从中选择一定数目的最佳复合。这是由限制星过程(boundstar过程)实现的。
(11)减稀疏性过程
减稀疏性过程(redustar过程)是减小星G(e|E0)中每个复合的稀疏性，从而得到简化星RG(e|E0)。因为星中的复合是最一般的，所以可能以过于一般的方式描述对象。例如在图7.8中复合
3减小为'3。本过程步骤是：第一步：确定初步的星G(e|ei)，ei∈E0。首先找到在e和ei中有不同值的变量。不失一般性，设这些变量是X1,X2,…,Xm，而且
ei =(r1,r2,…,rm,…,rn)。
则星G(e|ei)中有m个复合[Xj≠rj]，j＝1,…,m。在初步的星G(e|ei)中，复合的数目最多是n(因为m≤n)，最少是1(因为e≠ei，则 m≥1)。
第二步：确定完全的星G(e|E0)。设有|E0|＝k，先求出k个初步的星的逻辑积＆G'(e|ei)，ei∈E0，其中G'(e|ei)是星G(e|ei)中m个复合的析取。这是选择器的析取式的合取式，再化成选择器的合取式的析取式并化简。这些合取的析取就是复合的析取。这些复合的集合就是G(e|E0)。
第三步：对G(e|E0)中的复合进行减小和简化。力求减小每个复合，使其稀疏性减小，但还要覆盖已观察的事件。对每个复合，首先对复合中所有已观察事件进行合并操作，得到一个复合，再对这个复合进行一般化操作，得到一个简化复合。所有简化复合的集合就是简化星RG(e|E0)。
该方法的理论基础见Michalski(1975)。
(12)不相交化过程
不相交化过程又称为NID过程。它把非不相交复合的集合变成不相交复合的集合。如果输入不相交复合的集合，过程不起作用。过程的步骤是：
第一步：确定"核心"复合。把集合中多个复合同时覆盖的已观察事件放入多次覆盖事件表m-list。如果m-1ist空，则复合只是弱相交，即交集中只包含未观察的事件。这时过程结束。并指出复合的组合是弱相交的聚类。如果m-1ist不空，则对每个复合由在该复合中但不在m-1ist中的已观察事件进行合并操作，得到一个合并复合。这些合并复合称"核心"复合。
第二步：对m-1ist中的每个事件确定最佳的"宿主"复合。由m-1ist中取一个事件。把它分别放入k个核心复合中每一个。这是通过该事件分别与每个核心复合进行合并操作，得到k个修改的复合。用一个修改的复合代换相应的核心复合，就得到一种聚类。共可得到k种不同的聚类。用下面介绍的聚类质量准则评价k种聚类，选定并保存最佳聚类，去掉其它k-1种聚类。这个事件所在的核心复合就是它的最佳宿主复合。对m-list中每个事件重复上述过程，就把每个事件放入唯一的宿主复合中。最后得到k个不相交复合的集合。