|
7.3 类比学习
类比学习(Learning by Analogy)是获取新概念或新技巧的方法,它把类似这些新概念或新技巧的已知知识转换为适于新情况的形式。类比学习的第一步是从记忆中找到类似的概念或技巧,第二步是把它们转换为新形式以便用于新情况。例如人类的一种学习方式是先由老师教学生解例题(先例),再给学生留习题。学生寻找在例题和习题间的对应关系,利用解决例题的知识去解决习题中的问题。学生经过一般化归纳推出原理,以便以后使用。这种类比学习方式是人类常用的。
7.3.1类比学习问题求解的模型
这一节介绍通过类比学习进行问题求解。这就是对已知的解序列进行变换,以便得到适于新情况的新的解序列。另一方面,学习过程也是搜索过程,学习也是问题求解。这说明学习和问题求解是相关的两个方面,而且这里有两个不同层次的问题求解。下面介绍类比学习搜索空间的模型,这个搜索空间称为规划变换问题空间。
传统的中间结局分析(Means-Ends Analysis)空间包括下列内容:
1.可能的问题状态的集合。
2.一个初始状态。
3.几个目标状态(为简化假设只有一个目标状态)。
4.操作的集合,这些操作在一定前提下把一种状态转成另一状态。
5.计算两种状态间差异的差别函数,它一般用于求当前状态与目标状态的差异。
6.由差别函数查找操作的方法。
7.为使解有效而应满足的路径约束的集合,这些约束是对局部解序列的谓词,不是对状态和操作的谓词(考虑路径约束是对标准中间结局分析的改进)。
在这个空间中的问题求解是下列的标准中间结局分析:
1.比较当前状态与目标状态。
2.选择可以减小这个差异的操作。
3.如果前提满足就使用这个操作,否则保存当前状态,并用中间结局分析解决子问题,以便实现未满足的前提。
4.在解决子问题后,再取出保存的状态,继续处理原问题。
把类比学习作为问题求解时,使用推广的中间结局分析。我们要用类比学习由已知解序列得到新的解序列。这个过程有两步:提示过程和变换过程。
提示过程是寻找与当前问题类似的原有问题及其解路径。判定类似性的准则有下列四方面:
1.当前问题与原有问题的初始状态之间的差异。
2.当前问题与原有问题的目标状态之间的差异。
3.当前问题与原有问题的路径约束之间的差异。
4.满足当前问题的操作前提在全部前提中的比例,这称为候选解的可用性。
用于比较初始状态和目标状态的差别函数可以是标准中间结局分析中的差别函数,但最好使用相似矩阵这样的差别函数。用于比较路径约束的差别函数是问题状态差别函数的推广,它必须考虑操作序列的差别。计算相似性的更复杂方法是相对不变式体系。
变换过程是把原有解序列逐步变换成满足新问题的解序列。搜索一条解路径的过程是在状态空间的问题求解,这个搜索空间称为原始问题空间(原始空间)。变换过程是在另一个空间的问题求解,该空间称为变换问题空间(变换空间、T空间或规划变换问题空间)。变换空间的一个状态是原始空间的一个解路径。变换空间的初始状态是由提示过程找到的类似问题的解,其目标状态是由变换得到的满足新问题的解。变换空间的操作是基本的解变换。变换空间的差别函数应计算两个解的差异,它与提示过程的差别函数相同。图7.2给出变换空间和原始空间的示意图。
变换问题空间可以定义如下:
1.一个状态是原始空间中的一个解;
2.初始状态是由提示过程找到的类似问题的解;
3.目标状态是满足新问题的解;
4.操作称T操作,是把一个解序列变成另一解序列。常用的T操作有下列几种(注:说明中的操作是指原始空间的操作):
(1)插入--在解序列中插入新的操作。
(2)删除--由解序列中删除一个操作。
(3)顺序连接--如果原有解不满足新问题的前提,可以解一个子问题去满足该前提,再把子问题的解连接到原有解。
(4)保留子目标的代替--把原有解序列中的一个操作换成另一操作或操作序列。
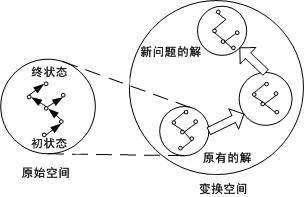 图7.2 原始空间和变换空间 |
(6)初始段连接--用中间结局分析求出从新的初始状态到原有初始状态的解,再连接到原有解的开始。
(7)序列合并--把两个原有解合并成一个操作序列。
(8)操作重新排序--重新排列原有解中的操作,以满足路径约束的新要求。
(9)参数替换--更换操作的对象。
(10)解序列修剪--去掉初始段或结尾段。
(11)序列倒排--完全倒排操作序列。
5.差别函数是差别矩阵DT,它是初始状态、目标状态、路径约束和可适用性这四方面差异的组合。变换过程应减小这四个差异。
DT=<Do(SI1,SI2),Do(SF1,SF2),Dp(PC1,PC2),DA (SOL1,SOL2)>
SI是初始状态,
SF是目标状态;
PC是路径约束;
SOL是解序列;
下标1表示找到的原有解;
下标2表示新问题要求的解;
DO是原始空间中状态间的差别函数;
DP是路径约束间的差别函数;
DA是原有解在新问题中的可适用性,这是原有解序列中不满足新问题中前提的操作所占的比例。
对DT的一种组合方式是四个分量的线性组合,另一种方式是△MIN方法(Carbonell,1980)。
6.由差别函数查找T操作的方法。T操作按一个启发函数排序,该启发函数表示T操作减小差异的效果。查找T操作方法的一个例子是:如果SOL1中的操作前提不满足,则选择"顺序连接"或"保留子目标的代替",以满足这个前提。
7.变换空间中没有路径约束。
在这个变换问题空间中,用中间结局分析方法找到一个T操作序列。类似问题的解经过这个T操作序列的变换得到新问题的解。