|
6.6.3 学习结果应用范围的扩展
机器学习得到的知识,应该既有用又有尽量大的适用范围。为此要考虑两个问题:可操作性和一般性。加州大学伯克利分校的Michells.Braverman和Stuart J.Russell研究了这个问题。
1.可操作性
提出可操作性问题的目的是希望学到的概念描述有利于提高系统运行效率。一种观点认为:如果一个概念描述能有效地用于识别相应概念的例子,则它是可操作的。但是概念描述不只用于识别例子,还可能用于产生例子等其它用途。而且系统性能不但有时间指标,还有空间指标等。因此,上述观点不完善。
R.M.Keller将可操作性定义如下:
如果给定:
(1)一个概念描述。
(2)一个执行系统,它利用概念描述改善执行情况。
(3)改善执行系统的各种要求,应明确各要求的类型和程度。
那么若满足下列二条件则该概念描述是可操作的:
(1)可用性:执行系统可以使用该概念描述。
(2)效用性:执行系统使用概念描述时,系统的运行得到要求的改善。
例如对Safe-to-Stack(x,y)的一个概括化解释结构如图6.23所示。
解释结构中的叶节点都是可操作的,如Made-of(x,m)和Spec-Grav(m,d)。某些中间节点也可能是可操作的,在图中的Density(x,d)是可操作的。于是得到图中的可操作性界限,图中虚线以下各节点是可操作的。对于可操作的中间节点,可以从解释结构中删掉它的子解释。如图中可删去Made-of(x,m)和Spec-Grav (m,d)。这称为"可操作性修剪"。图6.23的解释经过修剪后得到下列规则。
Volume(x,v)∧Density(x,d)∧X(v,d,w)
∧Isa(y,rect-solid)∧Made-of(y,lucite)
∧<(w,10) Safe-to-Stack(x,y)
2.解释学习的空间描述
R.M.Keller指出解释学习涉及三个不同的空间:例子空间、概念空间和概念描述空间。一个概念可由例子空间外延地表示成某些事例的集合。概念也可以由概念描述空间内涵地表示为例子空间例子的属性。图6.24说明了三个空间的关系。
概念空间指某个学习程序能描述的所有概念的集合,其中每个点对应例子空间的唯一的一个子集合。例如C1对应{I1,I2,I3}。但是概念空间中的一个点可以对应概念描述空间的多个点,这些点分成可操作的和不可操作的两部分。例如C1对应D1(不可操作的)和D2(可操作的)。对应同一概念的两个描述称为同义词。如D1和D2是同义词。解释学习的任务就是由不可操作的描述转化为可操作的描述。
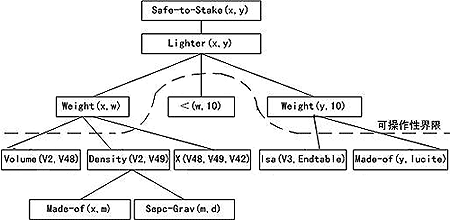 图 6.23 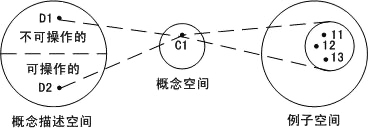
图 6.24 |
根据上述的空间描述,可以建立解释学习的一种模型。解释学习系统主要包括执行系统PS,学习系统EXL,领域知识库KB(这是不同描述间转换规则的集合)。令概念空间为C,概念描述空间为CD,例子空间为I。则系统工作过程如下。EXL的输入是概念C1的描述D1(一般是不可操作的)。根据KB中的知识,对D1进行不同描述的转换(这是一个搜索过程)。PS对每个转换结果进行测试,直到转换结果是PS可接受的描述D2(是可操作的)时,解释学习结束并输出D2。模型如图6.25。
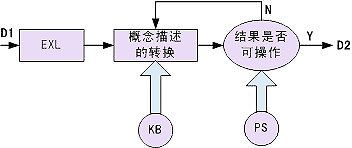 图6.25 解释学习的模型 |