第六章　实例学习

　　2． 一个实例
　　对积分∫3x・cosx・dx ，问题求解器产生出图 6.19所示的执行追踪。
图示

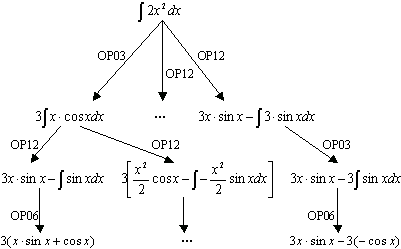图6.19 部分搜索树
　　评论器从中提取出几个示教例子：
　　∫3x・cosx・dxOP12 用u=3x 和dv=cosx dx （正例）
　　∫3・sinx・dxOP03 用r=3 和f(x)=sinx 　　（正例）
　　∫sinx・dxOP06 　（正例）
考虑对OP12的示教例子。如果这是它的第一个示教例子。由此得的变形空间就是
　　G=∫f(x)g(x)dxOP12, 用u=f(x) 和dv=g(x)・dx
　　S=∫3x・cosx dxOP12,用u=3x 和dv=cosx dx
　　如果第二个积分问题是∫5x・sinx・dx，则提取的示教例子是：
　　∫5x ・sinx dx=> OP12, 用u=5x 和dv=sinx・dx (正例)
　　∫5・cosx・dx =>OP03, 用r=5 和f(x)=cosx （正例）
　　∫cosx・dx=>OP10 (正例)
　　∫5x・sinx・dx =>OP12，用u=sinx 和dv=5x dx （反例）
利用这时里的OP12的一个正例和一个反例，修改变型空间为：
　　G={gl,g2},其中
　　　g1：∫polynom(x)・g(x)・dx=>OP12
　　　　　　用u=polynom(x) 和dv=g(x)・dx
　　　g2：∫f(x)・transc(x)・dx=>OP12
　　　　　　用u=f(x) 和dv=transc(x)dx
　　S={s1},其中
　　　s1：∫kx・trig(x)dx=>OP12
　　　　　　用u=kx 和dv=trig(x)dx
示教正例使常数3和5一般化为k(表示整数)，使sin和cos一般化为trig(表示三角函数)，结果为s1。示教反例导致两种可用的特殊化。在g1中，f被特殊化为polynom(表示多项式)，以防止u=sinx .在g2中，g被特殊化为transc(表示超越函数),以防止dx=5x odx 。这两个特殊化的结果都不覆盖反例。
　　用更多的示教例子，就可得到OP12的启发式规则，即开始给出的∫f(x)・transc(x)dx。