LEX是Thomas Mitchell (1981)设计的系统。它由经验学习简单的符号符积分问题。它的初始知识库有大约50种积分和化简操作。其中部分操作是：
　　　　　OP02　变 ∫x^rdx 为 x^r+1/(r+1)
　　　　　OP03　变 ∫rf(x) 为r∫f(x)dx
　　　　　OP06　变 ∫sinxdx 为-cosx
　　　　　OP08　变　1・f(x) 为f(x)
　　　　　OP10　变 ∫cosxdx 为sinx
　　　　　OP12　变 ∫udv 为uv -∫vdu
　　　　　OP15　变 ∫0・f(x)dx 为0
　　LEX 的目标是发现何时使用这些操作的启发式信息，即发现下列形式的产生式规则。
　　　　　<情况i>使用操作Opi
　　其中左边是与当前积分匹配的模式。例如OP12的启发式规则可能是：
　　　　　∫f(x)・transc(x)・d(x)
　　　　　以u=f(x) 和dv=transc(x)dx　用OP12
　　其中transc(x)表示超越函数
如果没有这些启发式信息，执行环节将在合法操作的空间盲目搜索。例如积分
　　　　　∫3x・cosx・dx
可以由OP12得到
　　　　　3x・sinx -∫3・sinx・dx
再由OP03得到
　　　　　3・sinx - 3∫sinx・dx
再由OP06得到
　　　　　3x・sinx - 3(-cosx)
它也以由OP03得到
　　　　　3∫x・cosx・dx
再由OP12得到
　　　　　3[x²/2・cosx - ∫-x²/2・sinx・dx]
这就误入了歧途。
　　学习启发式规则左边的任务可以看成是学习多个概念问题。LEX试图发现每个OPi 的适用情况，它追踪执行环节的行动，发现适用和不适用的操作，以此作为正例和反例，指导对规则空间的搜索。LEX用清除候选元素方法搜索规则空间，但对规则左边不一定找到唯一的模式。因此启发式规则的形式为：
　　　　　<以S和G集表示的变型空间> => 应用OPi
例如对OP12的启发式信息可能表示为下列的变型空间：
　　　　　G=∫f(x)・g(x)・dxOP12
　　　　　　　　令 u=f(x) 和dv=g(x)dx
　　　　　S=∫3x・cos x・dx=>OP12
　　　　　　　　令 u=3x和dv = cos x・dx
显然G过于一般，可能包含反例。S过于特殊，可能不覆盖某些正例。
　　1． LEX的结构
　　LEX包括四个互作用的程序，它的结构如图6.18所示。它符合学习多步任务的模型。

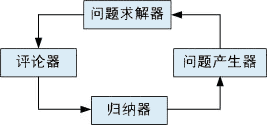图6.18 LEX的结构

　　"问题求解器"是执行环节，它使用当时的操作集和启发式信息解决符号积分问题，在成功地解决了一个积分后，"评论器"检查执行情况的追踪，对各步决策进行奖惩分配，从而提取出使用操作的正例(适当的)和反例(不适当的)。"归纳器"用这些示教例子来寻找启发式信息。最后，"问题产生器"检查知识库内容，由此产生新的积分问题，提交问题求解器解决。其中评论器和归纳器组成学习环节。