|
3.4.2 定性方程法
1.变量的定性值及其运算
若已知物理系统的微分方程、代数方程，首先需定义变量的定性值集合以及相应地定性运算，进而建立通常的运算转换为定性运算的方法。
定性值集合的元素是由对数轴的划分而得到的，通常最简单的办法是将(- ∞,∞)划分成(- ∞,0)，0,(0,∞)三段相应的定性值规定为－，0，+。这时定性值集合就是{－，0，+}。
变量x 的定性值记为[x]，定义为
[x]=
另外用
x表示
的定性值，即
定性值的加乘运算分别以
表示，可分别按下表定义：
 |
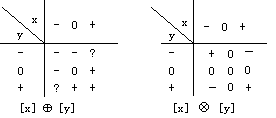表中出现的？表示不确定或无定义。
的运算规律：[0]
[e1]
[e1][0]
[e1][0][+]
[e1][e1][-]
[e1]-[e1]由+，×到? 的转换规律：
[e1+e2]
[e1][e2][e1×e2]
[e1][e2]依这些规律不难将代数方程、微分方程定性化。在得到定性方程后做出解释便是整个的定性推理过程。de Kleer 建立了一个ENVISION 定性推理系统。
2.举例 压力调节器定性分析
压力调节器是通过弹簧来控制阀门流量，以使流量为某设定值而不受流入的流量和负载变化的影响。
依物理学有
Q＝CA
P>0
其中Q为通过阀门的物质流量，P是压力，A是阀门开起的面积，而C是常系数，ρ是物质的质量密度。
依运算和转换规则容易得到定性方程
[Q]=[P]
Q=A+P(如果A>0)依物理上的一致性连续性原理还可建立其它定性方程。
由这些定性方程便可给出物理过程的定性解释。如可用定性方程描述该调节器的三种特殊状态：
OPEN 状态 A＝AMAX。这时定性方程为
[P]=0
P=0WORKING 状态 0<A<AMAX。这时定性方程为
[P]=[Q]
P+A=QCLOSED 状态 A＝0。这时定性方程为
[Q]=0
Q=0还可用定性方程讨论三种状态间的转换。