|
【章节小结】
在知识库中有大量的不完全的专家经验知识,这样的知识不可避免地带有模糊性、随机性、不可靠性或不知道等不确定因素。一般说来,不确定性是来自知识的客观现实和对知识的主观认识水平。人们在日常生活中要处理大量的不确定问题,现实世界中充满了大量的不确定性问题。
不确定性推理的模型包括不确定性的表示、计算和语义解释。
以产生式为知识表示的MYCIN系统中,证据的不确定性用CF表示, 规则A B的不确定性用CF(B,A)表示。PROSPECTOR系统规则的不确定性表示为(LS,LN),证据的不确定性表示为O(A)。与CF不同的是用两个参量LS、LN来表示规则不确定性,分别表明了A成立与A不成立对B成立的影响程度。证据理论是数学上更严谨的一种不确定性推理方法,证据理论可处理由不知道引起的不确定性,以信任函数Bel、似然函数PI来表示不确定性,不确定性计算主要依据基本概率函数m。
常识是人工智能研究的重要内容,常识和常识推理的形式化引起人工智能界的关注,常识推理的基本特征是在知识不完全的情况下进行的,不完全知识下的推理要求作出假设,对不知道的知识作一种猜测,随知识的增加可能出现证据,表明猜测不成立,要求修改所作的假设和相应的结论,这就是非单调性。非单调性刻画了常识推理的一般特征,非单调推理过程就是不断提出假设,进行标准逻辑下的推理,寻找不一致,进行回溯,消除不正确假设及其影响,进而再提出新的假设。
定性推理方法也是一种常识推理,仿照人类对物理现象的描述和解释来建立的。定性方程法、进程方法和定性模拟法是三种基本的定性推理方法。
【课后习题】
1. 已知
R1:A1→X CF(X,A1)=0.7
R2:A2→X CF(X,A2)=0.55
R3:X∧A3→Y CF(Y,X∧A3)=0.95
初始:
CF(A1)=CF(A2)=CF(A3)=1
CF(X)=CF(Y)=0
求CF(X),CF(Y)的更新值
2. 当A1,A2必然发生后,看X的概率变化,已知X的先验概率为0.02,而
R1:A1→X LS=25 LN=1
R2:A2→X LS=200 LN=1
求:O(X|A1),P(X|A1)
O(X|A1A2),P(X|A1A2)
3. 若A必然发生,X的先验概率为0.02,而规则
R1:A→X LS=90 LN=1
R2:X→Y LS=350 LN=0.001
又知P(Y)的先验概率为0.01,计算
P(Y|A)
4. 已知f1(A1)=0.7 f1(A2)=0.5 |V|=30 A1∧A2 B={b1,b2}
(c1,c2)= (0.4,0.5)
用证据理论计算f1(B)
5.从耶鲁射击问题
甲在时刻t1活着,乙在时刻t2>t1把子弹送入枪膛,乙在时刻t3>t2举枪对甲射击,问题:
甲在时刻t4>t3还活着吗?
来分析推理的非单调性。
6.举几个常识推理中非单调性的例子
7.求解定性方程组(如果有解的话)
8.求解定性方程组(如果有解的话)
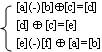
9.求解定性方程组(如果有解的话)
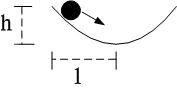
10.对一个在圆弧形槽内来回滚动的球进行定性分析