第三章 不确定和非单调推理方法

　　3.2.6 信含网络
　　信念（Belief）网络是一种模拟人类推理过程中因果关系的一种向图。它的结点表示问题求解中的命题或变量，也可以是假设，通过弧把认为有直接关系的命题或变量连结起来。若结点M的值直接影响结点N的值记作(M→N)，这时把M，N连结起来，而且连结强度用条件概率P(N|M)来表示。
　　一般说来，n个命题,…,之间相互关系的一般知识可用联合概率分布函数来描述，但十分复杂。Pearl 认为人在推理时知识并不是以联合概率分布形式表示的，而是以变量间的相关性和条件相关性表示，即用条件概率表示。如
　　P(,…,)=P(|-1,… ,)・(P(-1|-2,…,)・…・P(|) P()
　　例如图3.4所示
　　有P(,,…,x6)=P(x6|x5)・(P(x5|,x3)・P(x4|,)・(P(x3|)・P(|)・P()
图示

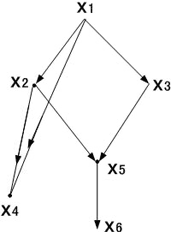图3.4信念网络
　　当命题间相关性由边表示，条件概率表示边的强度，从而命题间静态结构关系的有关知识就表示出来了。
　　当获取新证据新事实时，对每个命题可能取值的影响，将对每个结点定义一个信任度，记作BEL(x)。可规定
　　　　　BEL(x)=P(x=xi|D)
　　表当前所拥有的所有事实和证据D条件下，命题X取值xi的可信任程度。基于BEL进而计算新证据、事实下各命题的可信任程度。这便是不确定性计算问题。
　　信念网络是一种不确定的内涵表示。如何建立一种简单有效的方法来实现知识在网络中的传播是主要研究课题。