|
3.2.5 可性理论
Zadeh1965年提出了模糊集合论，在此基础上1978年又建立了可能性理论，并将不确定性理解为可能性。
1． 针对模糊概念建立模糊子集
一个概念常由其内涵来定义，而由其外延来表现出来，外延是具有内涵属性全体个体构成的集合。
对一个模糊概念（如年青、胖、高）也可用模糊集合来描述来表现。
设论域为U，其上定义了一个模糊概念
。如果对任意的u∈U依都规定一个数值μ
(u)∈[0,1]作为u以A的隶属程度，这时
μ
：U→[0,1]就叫U上
的隶属函数，定义了隶属函数的模糊概念称作U的一个模糊子集。用模糊子集来描述模糊概念。例如 U＝{a,b,c,d,e}，模糊概念为"圆块块"。
μ
：a→1
b→0.9 c→0.4 d→0.2 e→0模糊子集
=
( 1,0.6, 0.4, 0.2, 0) 或=(1/a+0.9/b+0.4/c+0.2/d+0/e 或
={(a,1),(b,0.9),(c,0.4),(d,0.2),(e,0)}
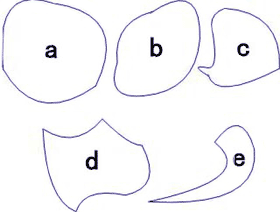便是"圆块块"这一模糊概念在U上的表现见图3.3。 |
 图3.3 |
当μ
的值域退化为{0,1}时，便退化为普通集合A了，这时的隶属函数就是普通集合A的特征函数了。给了模糊子集
，
便可定义并集、交集和全集，而且有μ
∪(u)=max{μ(u),μ(u)}μ
∩(u)=min{μ(u),μ(u)}μ
C(u)=1-μ(u)2.模糊推理举例
通常的假言推理是
A∧(A→B)→B
现在要讨论的是
与A→B中的A并不完全一致时，能否也可得到有价值的结论？设论域 U上有模糊子集
V上有模糊子集
而
→是U到V的一个模糊关系，即U×V上的一个模糊子集，其隶属函数定义为(
→)(u,v)=((u)∧(v))∨(1-(u))其中符号∨表示max，∧表min。
于是当已知有模糊子集
时，可得出1(v)=
u∈U((u)∧→(u,v))记作
1=!*(→)
 |
例如 |
| U＝V＝{1,2，3,4,5}，若u小则v大，已知u 较小，问v如何？ 若 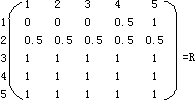表模糊概念小，1模糊概念较小，而表模糊概念大。而且知＝1/1+0.5/21＝1/1+0.4/2+0.2/3＝0.5/4+1/5可计算得 →的隶属函数为 进而求得 1=1・(→)=(1 ,0.4, 0.2 ,0 ,0 )・R =(0.4 ,0.4 ,0.4 ,0.5 ,1) 可理解为v较大。 |
3.U上模糊变量的可能性描述
设x是取值U的变量，对它可定义一个相容性函数，使x的每个取值都对应于[0,1]中的一个数。相容性函数就是对变量x的一种约束。特别当
是U上的模糊子集有隶属函数μA(x)时，可把与x联系起来，将μ(x)取作变量x的相容性函数，这时就是对x的一种约束了，如上例x表圆块块，这时便可说x=a的可能性为1，x=b的可能性为0.9,…。这样便给出了变量x的可能性分布，可记作poss(x=a)=1, poss(x=b)=0.9,…
值得注意的是poss与概率P是不同的。例如一个人早饭吃了x个鸡蛋的描述，x∈{1,2,3…}=U
| u= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| poss | 1 | 1 | 1 | 1 | 0.8 | 0.6 | 0.4 | 0.2 |
| P | 0.1 | 0.8 | 0.1 | 0 | 0 | 0 | 0 | 0 |
poss =(x=a∨y=b)=max{poss(x=a),poss(x=b)}
poss =(x=a∧y =b)=min{poss(x=a),poss(x=b)}
poss(x≠a)=1- poss(x=a)
若将不确定性以这种可能性来度量时，便可用可能性理论来讨论不确定性推理了。