第三章 不确定和非单调推理方法

　　3.2.3 证据理论
　　Dempster 和 Shafer 提出的证据理论，可用来处理不知道所引起的不确定性。采用信任函数而不是概率作为不确定性度量，通过对一些事件的概率加以约束来建立信任函数而不必说明精确的难于获得的概率，当这种约束限制为严格的概率时，证据理论就退化为概率论了。
　　1.证据的不确定性度量
　　若用U表示所有可能的假设集合，而U的元素间是互斥的。对任一AU，命题A表示了某些假设的集合（这样的命题间不再有互斥性）。针对医疗诊断问题， U就是所有可能疾病（假设）的集合，诊断的结果必是U中确定的元素构成的。A表示某一种（单元素）或某些种疾病。医生为了诊断所进行的各种检查就称作证据，有的证据所支持的常不只是一种疾病而是多种疾病，即U的一子集A。
　　首先在U的幂集2U上定义一个基本概率分配函数m：2U→[0,1]
　　满足　m(φ)=0
　　　　　 m(A)=1
　　m(A)表示了证据对U的子集成立的一种信任的度量，取值于[0,1]，而且2U中各元素信任的总和为1，不同于Bayes 方法，因为Bayes 方法仅对U中单个元素赋予一种信任�D�D概率。
　　信任函数
　　　　　Bel：2U→[0,1]
　　　　　Bel(A)= m(B)
　　即命题A的信任函数的值，是A的所有子集的基本概率分配函数会值的和，用来表示对A的总信任。知Bel(φ)＝0，Bel(U)=1 ,单元素集上m与Bel是相等的。
　　似然函数
　　PI：2U→[0,1]
　　Pl(A)=1-Bel(～A)=m(B)
　　表示不否定A的信任度，是所有与A相交的子集的基本概率分配函数值的和。
　　显然有，0 ≤ Bel(A)≤ Pl(A)≤ 1
　　而Pl(A)-Bel(A)表示了既不信任A也不信任～A的一种度量，可表示对不知道的度量，用区间（Bel (A),Pl(A)）来描述A的不确定性。Bel(A)表度量的下限，Pl(A)表度量的上限。实际上m,Bel,Pl只要知其一，必可求得另两个，但三个函数有不同含义。
　　几个特殊值
　　　(Bel(A),Pl(A))=(1,1)表示A为真，（这时Bel(A)=1,Bel(～A)=0）
　　　(Bel(A),Pl(A)=(0,0)表示A为假，（这时Bel(A)=0,Bel(～A)=1）
　　　(Bel(A),Pl(A))=(0,1)表示对A一无所知（这时Bel(A)=0,Bel(～A)=0）
　　对Bel(A)的计算也是容易的，如
　　Bel({a,b,c})=m({a,b,c})+m({a,b})+m({b,c})+m({c,a})+m({a})+m({b})+m({c})+m(φ)
　　需指出，m不是概率，因为
　　　　　m(A)≠ 1-m(～A)
　　如 U={a,b,c,d}，可规定m({a,b})=0.6,m(U)=0.4,而对U的其它子集的m值均为0。而在概率论中，若P({a,b})=0.6，那么{a,b}的余集的概率必为0.4。
　　除以区间(Bel(A),Pl(A)来作为证据A的不确定性度量外，还可以
　　　　　
　　来度量。其中|A|，|U|分别表示A和U所含元素个数。f1(A)具有性质
　　　　　f1(φ)=0,f1(U)=1,0≤f1(A)≤ 1 对AU。
　　2.规则的不确定性度量
　　设U={u1,…,un},A,B为U的子集，如
　　　　　A={a1,…,al}
　　　　　B={b1,…,bk}
　　那么可以(c1,…,ck)来描述规则A→B的不确定性度量，要求ci≥0,1≤i≤ k；cj≤1
　　3.推理计算
　　(1)f1(∧)=min{f1(),f1()}
　　　 f1(∨)=max{f1(),f1()}
　　(2)已知 f1(A),A→B (c1,…,ck)来计算f1(B)。
　　为求得f1(B),需先计算m(B),进而计算Bel(B),Pl(B)。
　　规定 m({b1},…,{bk})=(f1(A)・c1,…,f1(A)・ck)
　　　　　m(U) =1-f1(A)ci
　　便可得f1(B)。
　　(3)已知　→B (c1,…,ck)
　　　　　　 →B (c1',…,ck')
　　以及f1(),f1()如何计算f1(B) 。需先讨论对基本概率分配函数m1,m2在U上的合成 m=m1�m2
　　规定 m(Φ)=0
　　　　 m(A)=K・m1(X)・m2(Y)
　　其中X，Y为U的子集。(这种规定称作Dempster组合规则，要求m1,m2提供的证据满足某种独立性条件)
　　
　　若K-1≠0,这样的m就确定一个概率分配函数，而在K-1=0认为m1,m2矛盾，没有联合基本概率分配函数，常数K是根据m1�m2需对2U的所有元素的基本概率分配之和为1来确定的。
例题 例:
  　U={a,b,c,d}
　m1：{b,c,d}→0.7 U→0.3
　m2：{a,b} →0.6 U→0.4
　可列表求m =m1�m2
　　　　　
　于是 m1�m2：
　　　{b}→0.42，{a,b}→0.18,{b,c,d}→0.28
　　　U→0.12
　　　(K-1=m1(X)・m2(Y)=0.7(0.6+0.4)+0.3(0.6+0.4)=1)
　有了m1�m2便可计算Bel1�Bel2,如
　(Bel1�Bel2)({a,b})
　=m(B1)
　=m(Φ)+m({a})+m({b})+m({a,b})
　=0+0+0.42+0.18=0.60
　随之可计算Pl1�Pl2,从而可得f1(B)

　　4. 举例
　　(1) 已知 f1()=0.8,f1()=0.6
　　|U|=20 ∧→B={b1,b2} (c1,c2)=(0.3 ,0.5)来计算f1(B)
　　先计算 f1(∧)=min{f1(),f1()}
　　　　　　　　　　　=min{0.8,0.6}=0.6
　　进而计算 m({b1},{b2})=(0.6×0.3, 0.6×0.5)
　　　　　　　　　　　　 ＝(0.18,0.3)
　　于是有 Bel(B)=m(Φ)m({b1})+m({b2})+m({b1,b2})
　　　　　　　　 =0+0.18+0.3+0=0.48
　　(依ci定义，m({b1})=0.18,m({b2})=0.3,随之有m(U)=1-(0.18+0.3=0.52而对U的其他子集的 m 值均赋以零)
　　　　　PI(B)=1-Bel(～B)=1-0=1
　　最后得
　　
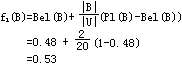
　　(2)已知 f1()=0.53,f1()=05.2,|U|=20。以及
　　　 →B={b1,b2,b3},(c1,c2,c3)=(0.1,0.5,0.3)
　　　 →B={b1,b2,b3},(c1,c2,c3)= (0.4,0.2,0.1) 求 f1(B)。
　　先求
　　m1({b1},{b2},{b3})=(0.53×0.1,0.53×0.5, 0.53×0.3)
　　　　　　　　　　　=(0.033,0.265,0.159)
　　m1(U)=1-(0.053+0.265+ 0.159)=0.524
　　m2({b1},{b2},{b3})=(0.52×0.4,0.52×0.2,0.52×0.1)
　　　　　　　　　　　=(0.208,0.104,0.052)
　　m2(U)=1-(0.208+ 0.104+ 0.052)=0.636
　　以及 m= m1�m2
　　K-1=m1({b1})m2({b1})+m1({b1})・m2(U)+m1({b1})・m2({b2})+m1({b2})m2(U)
+m1({b3})m2({b3})+m1({b3})m2(U)+m1(U)m2({b1}) +m1(U)m2({b2})+m1(U)・m2({b3})+m1(U)・m2(U)
　　　 =0.874
　　得
　　　
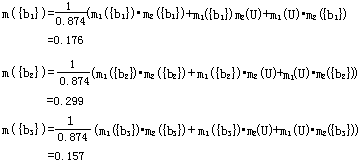
　　　m(U)=1-(0.176+0.299+0.157)=0.386
　　于是 Bel(B)= m({b1})+ m({b2}) +m({b3})
　　　　　　　 =0.632
　　　　 Pl(B)=1
　　最后得
　　　
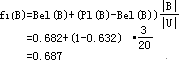
　　从代数观点看，MYCIN EMYCIN PROSPECTOR D-S给出的不确定方法均可构成半群；MYCIN D－S方法还有单位元但无逆元；EMYCIN　PROSPECTOR　方法既有单位元又有逆元，从而可构成群。