|
3.2.2 主观Bayes 方法
以语义网络表示的 PROSPECTOR 系统,采用了主观 Bayes 方法来度量不确定性。引入两个数值(LS,LN)来作度量,LS 表现规则成立的充分性,LN 表现规则成立的必要性,这种表示既考虑了 A 的出现对 B 的支持,又考虑了 A 的不出现对 B 的影响。
1. 对规则的不确定性度量
直接使用Bayes 公式来做度量时,在计算P(B|A)时需要已知P(A|B),为避开这个困难,提出了主观Bayes 方法。
对规则A→B的不确定性f(B,A)以(LS,LN)来描述。其中
下面分析一下LS,LN 的意义。
先建立几率函数
表示的是证据X的出现概率与不出现概率之比,显然随P(X)的加大O(X)也加大,而且
P(X)=0 时 O(X)=0
P(X)=1 时 O(X)=∞
这样,取值[0,1]的P(X)放大为取值[0,∞]便得O(X)。
不难验证
O(B|A)=LS・O(B)
O(B|~A)=LN・O(B)
由于
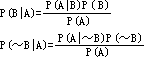
两者相比得
这就是
O(B|A)=LS・O(B)
相仿地也可得
O(B|~A)=LN・O(B)
由这两个公式可看出,LS表示A真时,对B为真的影响程度,表示规则A→B成立充分性。LN表示A假时,对B为真的影响程度,表示规则A→B成立的必要性。
几个特殊值

由LS,LN 的定义知,LS,LN均≥ 0,而且LS,LN不是独立取值的,只能出现LS>1,LN<1或LS<1,LN>1 或LS=LN=1。但不能出现两者同时>1或同时<1。
在实际系统中,LS,LN的值是由专家凭经验给出的,而不是依LS,LN的定义来计算的。
2.证据的不确定性度量
就以O(A)或P(A)表示证据A的不确定性,转换公式是
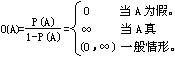
3.推理计算
(1) 当A确定必出现时,可直接使用
O(B|A)=LS・O(B)
O(B|~A)=LN・O(B)
以求得使用规则A→B后,O(B)的更新值O(B/A),O(B/~A)。若需要以概率表示,再由
计算出P(B|A),P(B|~A)。
(2)当A是不确定的,即P(A)≠1时,需作如下考虑。
设A'代表与A有关的所有观察,对规则A→B来说 Duda 1976年给出公式
P(B|A')=P(B|A)・P(A|A)'+P(B|~A)・P(~A|A')
问题是当P(B|A'),A→B (LS,LN)以及P(B)已知时,如何更新P(B)或说寻求P(B|A') 。
当P(A|A')=1时,证据A必然出现有
不难验证这公式是成立的。
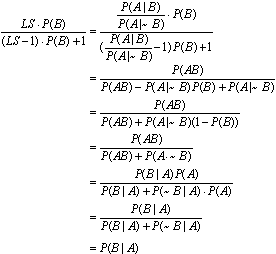
当P(A|A')=0时,证据A必然不出现经同样的推导得
当P(A|A')=P(A)时,也即观察A'对A无影响。有
P(B|A')=P(B|A)・P(A)+P(B|~A)・P(~A)
=P(BA)+P(B・~A)
=P(B)
这样已可确定P(A|A')为0,P(A),1时相应的P(B|A')的值,便可得线性插值图见图3.1。
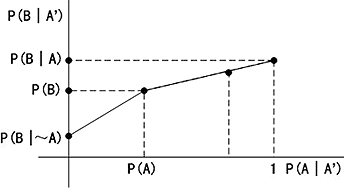 图3.1 线性插值图 |
(3) P(
P(
(4) 若
4.举例
当证据
R1:
R2:
R3:
R4:
下面进行计算。
(1)依P(B)=0.03 便得
(2)依R1,有
O(B|
(3)依R2有
O(B|
由于
当证据A必然发生,已知
R1:A→
R2:
又知P(
(1) 依A必发生,由R1得
P(
(2) 设P(
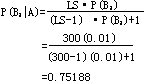
(3) 设P(
求得
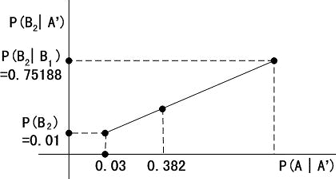 图 3.2 |