|
3.2 不确定推理方法
3.2.1 确定性方法
以产生式作为知识表示的MYCIN中，第一次使用了不确定性推理方法，给出了以确定性因子或称可信度作为不确定性的度量。
1.规则的不确定性度量
规则以A→B表示，其中前提A可以是一些命题的合取或析取。MYCIN系统引入可信度CF作为规则不确定性度量。CF表示了增量
P(B│A)－P(B)
相对于P(B)或P(～B)的比值。其中P表概率。规定
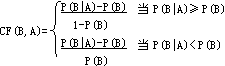
CF(B，A)表示了证据A为真时，相对于P(～B)=1-P(B)来说A对B为真的支持程度（当CF(B,A)≥ 0）。或相对于P(B)来说A对B为真的不支持程度（当CF(B,A)<0）。这种定义形式保证了－1≤CF(B,A)≤ 1。当P(B│A)－P(B)相同时，P(B)小的CF小，P(B)大的CF大。
容易看出CF(B,A)的几个特殊值：
（1） 前提A真，结论B必真的情形。由P(B│A)＝1来体现，这时CF(B,A)=1。
（2） 前提A与结论B无关的情形。由P(B│A)＝P(B)来体现，这时CF(B,A)＝0。
（3） 前提A与结论B无关的情形，由P(B│A)＝0来体现，这时CF(B,A)＝－1。
显然CF(B,A)≥ 0表示前提A真支持B真。CF(B,A)＜0表示前提A真不支持B真。
不难看出，CF(B,A)的定义借用了概率，但它本身并不是概率。因为CF(B,A)可取负值，CF(B,A)+CF(B,～A)不必为1甚至可能为0。
实际应用中，A→B的CF(B,A)值是由专家主观确定的，并不是由P(B│A)，P(B)来计算的。需注意的是CF(B,A)表示的是增量P(B|A)－P(B)对1－P(B)或P(B)的比值，而不是绝对量的比值。
2.证据的不确定性度量
证据A的不确定性也可以CF(A)表示，同样规定－1≤CF(A)≤ 1。
几个特殊值规定为
（1） A肯定为真时CF(A)＝1。
（2） A肯定为假时，CF(A)＝－1。
（3） 对A一无所知时，CF(A)＝0。
CF(A)>0 表示A以CF(A)程度为真。
CF(A)<0 表示A以CF(A)程度为假。
实际使用时，初始证据的CF值由专家提供，其它证据的CF值是需使用规则经推理求得。
3.推理计算
（1） 已知 CF(A),A→B CF(B,A)求CF(B)
规定 CF(B)＝CF(B，A)・max{0,CF(A)}
（2） 规定 CF(～A)＝-CF(A)
CF(
∧
)＝min{CF()，CF()}CF(
∧)=max{CF(),CF()}（3） 由规定
→B求得CF(B)，又使用规则→B时，如何更新CF(B)。或说已知 CF(
)，CF()以及CF(B,)，CF(B,)来寻求合成的CF(B)。依（1）先计算出
CF1(B)＝CF(B，
)・max{0,CF()}CF2(B)＝CF(B,
)・max{0,CF()}进而规定
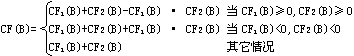
CF(B)的更新计算，也可这样来理解。已知CF(A)，A→B CF(B，A)而B原来的可信度为CF(B)，来求B的可信度更新值CF(B|A)。这时的计算可写成
当CF(A)＝1时，有
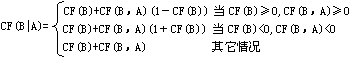
当CF(A)<1(证据A也是不确定的)，这时CF(B|A)必然比CF(A)=1时的CF(B|A)来得小。若CF(A)>0，可以CF(A)・CF(B，A)作为对规则A→B的可信度，而CF(B|A)的计算仍可使用CF(A)=1时的公式。但CF(A)<0时，规则A→B可不使用，像MYCIN系统规定CF(A)≤0.2就认为是不可使用的前提。
关于CF(B|A)的计算，对除CF(A)，CF(B，A)均非负，以及CF(B)，CF(B，A)均为负之外的其它情形，EMYCIN系统使用的是
应指出，若通过引入信任增长度MB和不信任增长度MD来定义CF=MB-MD，并用MB、MD来计算合成的CF值，半群代数结构方可得到保证。而在MYCIN中上述计算CF(B|A)的方法过于简单了，并不能保证CF合成计算的结合律了。
4. 对CF定义的改进
确定性因子直观上应满足下述性质：
(1) CF(B,A,e)=CF(B,A) 独立性
(2) CF(B,
,)=CF(B,,)组合交换性(3) 若CF(A,A')=1 则CF(B,A)=CF(B，A')有序组合性
其中e是在已知证据A之前出现的证据。
但上述所定义的CF(B,A)并不满足这些性质。例如 已知
→B
CF(B，)=0.9,→B
CF(B,)=-0.9来计算P(B|e)。依CF(B，A)定义有
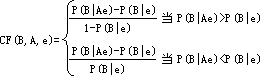
于是由
有0.9=(P(B|
e)-P(B|e))/(1-P(B|e))若规定P(B|e)=0.5，可得
P(B|
e)=0.95进而由
有-0.9=(P(B|
e)-P(B|e))/(P(B|e)依P(B|
e)=0.95得P(B|
e)=0.10我们若先对
再对重复计算过程得P(B|
e)=0.90从而出现了P(B|
e)与P(B|e)不相等情形，这与人们的直观认识不一致。Heckerman 修正了对CF的定义记为CF*解决了CF应满足的直观性质。规定
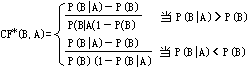
5.举例
已知 R1：
→
CF(
,)=0.8R2：
→
CF(,)=0.5R3：
∧
→
CF(,∧)=0.8初始证据
,,的CF值均设为1，而初始未知证据,的CF值设为0，也即认为对,是一无所知。来计算CF(
),CF()的更新值。依R1，CF(
|)＝0+0.8(1－0)＝0.8 即使用R1后的CF()由0提高到0.8了。依R2，CF(
|)=0.8+0.5(1-0.8)=0.9依R3，需先求
CF(B∧
)=min
(CF(),CF())=min (1,0,9)=0.9
而
∧→
的前提CF(∧)≠1,要作CF(，∧)×CF(∧)=0.8×0.9=0.72再计算CF(
|∧)=0+0.72(1-0)=0.72这样便求得了CF(
)，CF()分别为0.9和0.72。