|
一个人工智能系统,由于知识本身的不精确和不完全,常采用非标准逻辑意义下的不确定性推理方法和非单调推理方法。对于不确定推理来说,不精确性如何描述以及如何传播是主要问题,对于非单调推理来说,如何提出合理的假设以及矛盾的处理是主要问题。
这一章介绍几种不确定、非单调推理方法,同时对定性推理也作简要讨论。
3.1 概述
3.1.1 不确定推理
知识库是人工智能系统的核心,而知识库中的知识既有规律性的一般原理,又有大量的不完全的专家经验知识,这样的知识不可避免的带有模糊性、随机性、不可靠或不知道等不确定因素。一般地说,不确定性是来自知识的客观现实和知识的主观认识水平。不确定性是人们思维过程中经常出现的一种心理状态,人们在日常生活中要处理大量的不确定性问题。现实世界上几乎没有什么事情是完全确定的,处理不确定性的目的是希望得到对某一命题的精确判断。
1.不确定性问题的代数模型
一个问题的代数模型是由论域、运算和公理组成的。依这种观点,我们希望所引入的各种不确定推理方法应符合某种代数结构,如在某种意义下构成半群(在不确定性值域上,对不确定性度量的合成运算来说,具有封闭性并满足结合律),甚至反过来把这种结构做为建立一种不确定推理方法的必要条件。以这种观点建立的不确定问题模型必须说明不确定知识的表示、计算和语义解释这三个方面。
表示问题 指的是采用什么方法描述不确定性,这是解决不确定推理的关键一步。通常有数值表示和非数值的语义表示方法,两者都不完善。数值表示便于计算、比较,再考虑到定性的非数值描述才能较好的解决不确定问题。如对规则A→B和命题(事实)A 分别以f(B,A)和C(A)来表示不确定性度量。
计算问题 主要指不确定性的传播和更新,也即获得新的信息的过程。包括:
(1) 已知C(A),A→B f(B,A) 如何计算 C(B)。
(2) A的度量
(3) C(
当然初始命题的不确定性度量的获得也是重要的,这常常是主观确定的由有关领域的专家给出。
语义问题 指上述表示和计算的含义是什么?即对它们进行解释。目前只有概率方法
较好地回答了这个问题。
有如对f(B,A)可理解为当前提A为真时对结论B为真的一种影响程度,C(A)可理解为A为真的程度。特别关心的f(B,A)的值:
(1) A真则B真,这时f(B,A)=?
(2) A真则B假,这时f(B,A)=?
(3) A对B没有影响时f(B,A)=?
对C(A)关心的值是:
(1) A真时,C(A)=?
(2) A假时,C(A)=?
(3) 对A一无所知时,C(A)=?
2.不确定推理方法的分类
不确定推理方法可分为形式化方法和非形式化方法。形式化方法有逻辑法、新计算法和新概率法。逻辑法是非数值方法,采用多值逻辑、非单调逻辑来处理不确定性。新概率法不足以描述不确定性,从而出现了Dempster-Shafer 方法、确定性因子法以及模糊逻辑方法。新概率法试图在传统的概率论框架内,采用新的计算工具以适应不确定性描述。非形式化方法,是指启发式方法,对不确定性没有给出明确的概念。
这种度量法是着眼于语法上的不同,着眼语义上的不同可分为外延式方法和内涵式方法。外延式方法(也称产生式系统)把不确定性看成是一种广义的真值,一个公式的不确定性是由其各子公式的不确定性的计算来确定,其代表是MYCIN系统。内涵式方法(也称基于模型的方法)把不确定性看成一种状态或可能世界的子集,其代表是概率论方法,一般采用网络结构来表示。
还一种观点,把处理不确定问题的方法分为工程方法、控制方法和并行确定性法。工程法是将问题理想化忽略那些不确定因素。控制法是利用控制策略来消除不确定性的影响,如启发式搜索方法。并行确定性法是把不确定性推理分解为两个相对独立的过程:一个过程不计不确定性采用标准逻辑进行推理;另一个过程是对第一个过程的结论加以不确定性度量,前一过程决定信任什么,后一过程决定对它的信任程度。
不确定推理方法是70年代提出并加以研究的,实际的人工智能系统采用的不确定推理常是不够严谨的,但尚能解决些问题,符合人类专家的直觉,在概率上也可给出某种解释。
Shortliffe 等人1975年结合MYCIN系统的建立提出了确定性理论。Duda等人1976年结合PROSPECTOR 系统给出了主观概率法。Dempster Shafer1976年提出证据理论。Zadeh 1978年提出了可能性理论,1983年提出了模糊逻辑。Bundy 1984年提出了关联值计算。Cohen 1985年讨论一种非数值方法称作批注理论。Nilsson 1986年提出概率逻辑。Pearl 等人1986年信任网络。
3.直接使用Bayes公式的方法
不妨以医疗诊断为例来说明,设有几种疾病B1,…,Bn而症状为A,问题是判断在症状A下患者得了什么病?其可信任程度如何?这个问题可直接引用Bayes公式来求解。
Bayes 公式:
设有事件 B1,…,Bn 互不相容, B1∪B2…∪Bn =Ω(全集),事件A能且只能与 B1,…,Bn 中的一个同时发生,而且P(A)>0,P(Bi)>0 i=…n 。则有
P(Bi|A)=
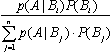 i=1…n
i=1…n这公式将症状A出现后患病Bi的概率计算化为P(A|Bi)和P(Bi)的计算了。如果将A出现下可能患有疾病Bi的不确定性度量就视作条件概率P(Bi|A),使可依Bayes 公式进行计算了。当某个K下,P(Bk|A)明显地大,便可认为病症A下患者得了Bk型疾病,其可信程度就是P(Bk|A)。
这种计算方法直接、明了,然而要求 B1,…,Bn 相互无关,这实际上是难于得到保证的,而P(A|Bi)和P(Bi)的计算也常是有困难的,于是Bayes公式的方法还不能直接使用需另作研究。