第二章 归结推理方法

　　2.7.2 Mating 法
　　Mating 推理方法是Andrews 提出的，与归结法有相同又有不同之处。
　　归结方法的主要问题之一是需将有关公式依分配律化成子句形。如
　　　　P∨(Q∧R)=(P∧Q)(P∧R)
　　然而这带来了新的问题，文字P在公式左端仅出现一次而在右端的子句形中都出现了两次，自然对归结推理过程是不利的。
　　像Church类型定理：f是一个函数，A和B是f的定义域的子集，那么A和B并集A∪B在f 下的映象必等于A，B在f下映象的并集。这定理的形式描述只出现20个文字，但其子句形则有104个文字出现了。而且子句化后原定理的基本逻辑结构也消失了。
　　自然演绎法虽有不少优点，但和归结法一样也要将原公式"打碎"，这样将注意力集中于各个子公式上面看不到整体结构。
　　Mating 方法不化成子句形又有整体观念。
　　我们结合一例子来说明这种方法的推理步聚。
例题 例:
  　证明　(x)(y)(P(x)←→P(y))→((x)P(x)←→(y)P(y))
　证明步骤：
　(1) 将要证的定理取否定，消去→、←→（这同归归结法）。
　　(x)(y)[(～P(x) ∨ P(y)) ∧(～P(y) ∨P(x))]
　　∧ [(x)P(x) ∧(y)～P(y)] ∨[(y)P(y) ∧ (x)～P(x)]
　(2) SKOLEM　化消去存在量词
　　(y)[(～P(c) ∨ P(y)) ∧(～P(y) ∨P(c))]
　　∧ [P(d)∧～P(e)] ∨[(z)P(z) ∧(x)～P(x) ]
　　（不同于归结法的是没有前束化和再作合取范式而得子句形）。
　(3) 列写二维表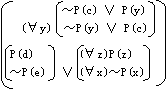
　　　　
　表中水平方向公式间是析取关系，垂直方向公式间是合取关系。这种表给出了公式的总体结构，观察起来也是方便的。
　(4) 变量二倍化例化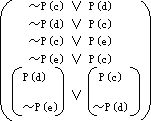
　　　　
　这一步包括二倍化（按需要可进行多次）
　(y)((～P(c) ∨P(y)) ∧(～P(y) ∨P(c)))
　=(y)((～P(c) ∨ P(y)) ∧(～P(y) ∨ P(c)))
　∧(y)((～P(c) ∨P(y)) ∧(～P(y) ∨P(c)))
　变量易名使无共同变量
　(y)((～P(c) ∨P(y)) ∧(～P(y) ∨P(c)))
　∧(w)((～P(c) ∨ P(w)) ∧(～P(w) ∨ P(c)))
　∧(P(d)∧～P(e))∨((z)P(z)∧(x)～P(x))
　再消去全称量词，在置换θ＝{d/x,d/y,c/z,e/w}下便得上面的例化后的二维表。
　(5) 判断例化后二维表的矛盾。
　可以一个更简单的例子来说明，二维表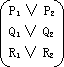
　　　　
　相当于公式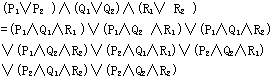
　
　要说明这公式为假，必须所有的合取项均为假，也即每个（・∧・∧・）项中都含有互补对。这直接由二维表观察过P1的四条路径，P1，Q1，R1 ；P1，Q1，R2；P1，Q2，R1；P1，Q2，R2；来检验是否有互补对，对过P2的四条路径也同样要求。这样寻求矛盾的方法就避免了化成子句所带来的不方便。如果二倍化例化尚找不到矛盾，需做新的多倍化例化。只要定理成立总能用这种方法找出矛盾的。