第二章 归结推理方法

　　2.7 非归结方法

　　包括采用了各种控制策略的归结推理过程，仍然避免不了产生大量的归结式，使得归结法还不能处理复杂问题，甚至对人来说较容易得到的一些结果也难于使用归结法得到证明。
　　从归结法本身来看，采用的是以消去联结词→而引入子句形为出发点的，这是不自然的。因为以P→Q的形式描述因果关系比以子句形～P∨Q要直接，或说子句描述失去了因果信息。再者，子句形描述将定理的条件和结论完全同一化了，无法区分了，这给推理过程引入启发信息人－机交互带来了困难。
　　由于归结法的弱点，导致人们研究非归结方法，70年代就出现了以Bledsoe的自然演绎法为代表的一些推理方法。

　　2.7.1 Bledsoe 自然演绎法
　　自然演绎法是效率较高的一种推理方法。如微积分中连续函数的和仍连续的定理，采用归结法归结出10万个子句尚无结果，而使用了Bledsoe自然演绎法仅27步就得到了证明。
　　这种方法是保留了联结词→下进行推理的。
　　消去量词仍是重要的，与归结法不同的是要消去全称量词（"x），而消去量词后的公式的变量认为是在存在量词作用下的。
　　自然演绎法引入了多条推理规则，这也是效率高的原因之一，不像归结法那样仅使用一条归结推理规则，规则形式常是要找置换θ，使得某公式在θ下成立，从而有…结论。这同公式中的变量受存在量词作用是有关的。
　　推理过程不是反演法，不要化成子句形，从而目标与条件是明显地区分开来了。将问题依推理规则化成一些子问题来证明。
　　1． 一些简单公式的标准化
　　有如归下的SKOLEM标准形，这里我们称为SKOLEM*标准形
原公式 SKOLEM*标准形
(x)P(x)
 P(x)
Q→(x)P(x) Q→P(x)
(x)(Q→P(x)) Q→P(x)
(x)P(x)→C P(x)→c
(x)P(x) P(x0)
Q→(x)P(x) Q→P(x0)
(x)(Q→P(x)) Q→P(x0)
(x)P(x)→C P(x0)→c
(x)(y)P(x,y)→C P(x,g(x))→c
H→(u)(v)Q(u,v) H→Q(u,h(u))
(x)(y)P(x,y)→(u)(v)Q(u,v) P(x,g(x))→Q(u,h(u))
(y)(x)P(x,y)→(v)(u)Q(u,v) P(x,y0)→Q(u,v0)
　　SKOLEM*标准形中保留了联结词→，而且也没要求化成前束形。其中的g(x),h(u)等仍称作为SKOLEM 函数。所得的SKOLEM*标准形中的变量认为是受存在量词作用的。
　　2． 符号规则
　　为对一般公式SKOLEM*标准形，需定义公式的正负概念以及公式间的符号规则。
　　对一个公式E来说，其正负如何依赖于它的子公式的正负，有如下规定：
　　(1)如果A∧B是正(负)，那么A和B均为正(负)。
　　(2)如果A∨B是正(负)，那么A和B均为正(负)。
　　(3)如果～A是正(负)，那么A是负(正)。
　　(4)如果A→B是正(负)，那么A是负(正)而B是正(负)。
　　(5)如果(x)A是正(负)，那么A是正(负)而是正(负)量词。
　　(6)如果(x)A是正(负)，那么A是正(负)而是负(正)量词。

例题 例:
  　设E＝(H→(C→～D))→(～A∨(B→F))
　若E是正（总是这样设定），由(4)
　(～A∨(B→F))为正，(H→(C→～D))为负。
　再依(2)有　～A,(B→F)为正
　依(4)有　H为正，(C→～D)为负。
　最后依(4)(3)有　A，B，C为负，F，～D为正。
　　 3． 消量词规则
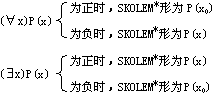
　　(1) 对只有一个量词的简单公式，规定
　　　
例题 例1:
  　Q→(x)P(x)
　先设为正，依符号规则Q为负而(x)P(x)为正，从而(x)P(x)应化为P(x)。
　于是Q→(x)P(x)的SKOLEM*形为
　　Q→P(x)
例题 例2:
  　(x)P(x)→C
　先设为正，依符号规则(x)P(x)为负，从而(x)P(x)的SKOLEM*形为P(x0)
　于是(x)P(x)→C的SKOLEM*形为
　　 P(x0)→C
　　(2) 一般情形（不含情形(1)），若公式E中变量x由正量词所约束，而该量词左边所有负量词为
　　　　
　　当r=0时，则x以常量代入。
　　当r≠0时，则x 以f(,…,)代入，其中f是E中未出现过的函数符号。
　　对E中所有变量依次做这样的代入，便可消去全部量词，便得E的SKOLEM*形。
例题 例3:
  　E＝(x)(y)P(x,y)→(u)(v)Q(u,v)
　设E为正，有
　(x)(y)P(x,y)为负，从而(x)为负，(y)P(x,y)也为负，于是(y)为正，这样变量y为正量词所约束，而(y)左边有负量词(x)，从而(x)(y)P(x,y)应化为P(x,f(x))。又有(u)(v)Q(u,v)为正，从而(u)为负，(v)为正。这样v是正量词所约束的，而(v)左边有负量词(u),从而(u)(v)Q(u,v)应化为Q(u,g(u))。
　故E的的SKOLEM*形为　P(x,f(x))→Q(u,g(u))

　　4.推理规则
　　自然演绎法不同于归结法的反演推理法，是直接来证明公式的成立。例如要证明(x)P(x),只需论域中有个x0，使P(x0)成立。在这种观点下，把(x)P(x)化成了SKOLEM*形，得P(x)而认为x是受存在量词约束。这种理解下可引入一条推理规则，若有置换θ使Pθ为真就有P(x)为真。也即(x)P(x)得证。这样就不难理解下述规则了。符号[E]，表示规则应用于E是成立的。
　　(1) MATCH：[H→C]
　　如果Hθ＝Cθ　则θ为所求。
　　这是最简单的规则了，要求目标C同假设H匹配，如果找到一个置换θ使Hθ＝Cθ 。
例题 例:
  　P(x)→P(a) (已是SKOLEM*形)是成立的，因θ＝{a/x}下有
　　P(x)θ =P(a)θ
　这个θ可通过合一算法求得。
　　(2) AND－SPLIT：[H→A∧B]
　　如果[H→A]在θ下而[H→Bθ]在λ下成立则θ・λ为所求。
例题 例:
  　P(x)→P(a)∧(Q(x)→P(a)) (已是SKOLEM*形)成立。因有θ＝{a/x}和λ＝{a/x},使
　[P(x)→P(a)],[P(x)→(Q(a)→P(a))]成立。
　　(3) CASES：[H1∨H2 →C]
　　如果[H1→C]在θ下，而[H2θ→C] 在λ下成立，则θ・λ为所求。
　　(4) OR－FORK：[A∧B→C]
　　如果[A→C]在θ下成立则θ为所求，否则需证[B→C]成立。
　　(5) BACK-CHAIN:[H ∧(A→B)→C]
　　如果[B→C]在θ下，而且[H→Aθ]在λ下成立则θ・λ为所求。
　　我们仅介绍这几条规则。
　　5． 举例
　　使用自然演绎方法来证明
　　　　(P(a)∧( x)(P(x)→Q(x))→Q(a)
　　先将这公式化成SKOLEM*形　
　　　　(P(a) ∧(P(x)→Q(x)))→Q(a)
　　依规则BACK-CHAIN,有θ＝{a/x},使
　　　　Q(x)θ →Q(a)θ ,即Q(a)→Q(a)
　　令λ空置换，有
　　　　P(a)λ →P(x)θ・λ 即P(a)→P(a)
　　成立。从而有　θ・λ＝θ＝{a/x},使　
　　　　(P(a) ∧ (P(x)→Q(x)))→Q(a)
　　成立。