|
2.6.2 Horn 子句
语句 B←
，…，
和B←都是仅有一个正文字B的子句，称作定子句，而目标语句←，…，是没有正文字出现的子句。定子句和目标子句统称Horn子句，也即最多含有一个正文字的子句是Horn子句。Horn子句有着广泛的应用，是1951年由逻辑学家Alfred Horn提出来的。
这样，Prolog 语句都是Horn 子句。
一个由Horn子句构成的子句集称作Horn 子句集。Horn子句类是一阶谓词公式的真子集，但有与一阶逻辑的同样的表达能力。
一个非Horn 子句集S，可通过变换化成Horn子句集S'，使S'不可满足等价于S不可满足。对Horn 集来说，如果S是不可满足的，那么存在从S到□的不使用因子的正单元归结和输入归结。但不保证有正单元输入归结。
 |
例: |
| S={P∨Q,～P∨Q,～P∨～Q,P∨～Q} 其中P∨Q非Horn子句从而S不是Horn集 。依 2.3.4 的分离规则，得 S'＝{Q，～Q} S″={Q,～Q} 有S不可满足等价于S'、S″同时不可满足。而且S'、S″均为Horn 子句集 |
2.6.3 SLD（有选择的线性）归结
由一个目标子句和若干个定子句组成的子句集称作定子句集，SLD归结是定子句集上的一种线性归结，从目标子句C0开始的，Ci是Ci-1与S中某定子句的归结式。可证明定子句上的SLD是完备的。
Prolog 解释过程采用的是受限的SLD归结，每次归结总是从目标子句最左边
文字开始的，而且依次同定子句作归结（宽度优先），当全部定子句均不能与当前目标子句最左边文字作归结时，引起回溯，选定当前目标子句的下一个文字为被归结文字。
 |
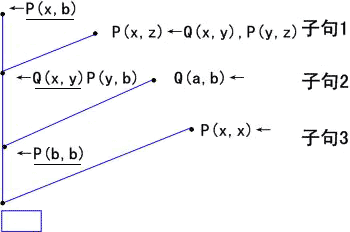 图2.5 Porolog 中采用的SLD归结 
图2.6 深度优先的SLD归结 |
|
例: |
| 已知 (1) P(x,z)←Q(x,y),P(y,z) (2) P(x,x)← (3) Q(a,b) 目标为←P(x,b) 归结过程见图2.5和2.6 |