第二章 归结推理方法

　　2.4.4 归结法的完备性
　　对于给的定理来说，我们使用归结方法建立了推理证明过程。问题是：若定理成立，是否使用归结方法必能得到证明呢？或对一个公理体系来说，使用归结法能推出的定理和所有成立的定理个数上看少不少？这就是归结法的完备性（值得注意的是完备性还有其他的理解）。结论是归结法是完备的。对一个推理方法而言尽管不是完备的，但能推出相当一部分定理，而且效率也较高，仍是可取的。一个推理方法提出后，困难的往往是完备性的证明，如一阶逻辑的公理系统的完备性就不容易证明。归结法完备性证明要使用 Herbrand 定理，从这个意义上说，归结原理是建立在 Herbrand 定理之上的。
　　1． 归结与语义树"倒塌"过程
　　我们以一个简单的例子来说明，对子句集S和相应的语义树T，当将S的任意两子句的归结式加入S后，相应的语义树T(1)较T"倒塌"了两个分枝，随着不断地归结T就不断地"倒塌"，当S是不可满足的T将倒塌成只剩下根结点了。
例题 例:
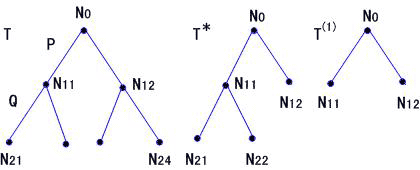
  　　S＝{P,～P∨ Q,～P∨～Q}
　　A＝{P,Q}
　画出语义树T和相应的封闭树T*见 图2.4
图示

图2.4语义树倒塌
　　归结过程
　　（1）P
　　（2）～P∨ Q
　　（3）～P∨～Q
　　（4）～P 　　　(2)(3)归结
　　（5）□　　　　(1)(4)归结
　　从树T*上看，先观察N11结点，有子结点N21，N22对应的
　　I(N21)={P，Q}　　使子句（3）为假。
　　I(N22)={P，～Q}　使子句（2）为假。
　　从而N21，N22都是失败结点，因I(N11)＝{P}不会使S的子句为假。N11的特点是它有两个分枝对应的子结点N21，N22都是失败的结点，这时相应的子句(2)(3)必可做归结，有归结式～P。
　　进而将～P并入S得S∪{～P}，这时的I(N11)={P}，已使 S∪{～P}的子句～P为假了。从而N11是S∪{～P}的语义树(同T)的失败结点了，其封闭树为T(1)。这就是说作一次归结，就使封闭语义树倒塌两个分枝N11N21，N11N22，或说N11N21， N11N22被剪枝了。
　　对T(1)的结点N0，有两个分枝对应的子结点N11，N12都是S∪{～P}的失败结点，又
　　I(N21)={P}　　　使子句（4）为假
　　I(N22)={～P}　　使子句（1）为假
　　这时子句（1）（4）又可做归结，有归结式□。
　　将□并入S∪{～P}得S∪{～P,□},N0已是失败结点，其封闭树为T(2)，是只剩下根结点N0的树了。
　　这个例子说明归结过程同语义树的倒塌过程是一回事。从而启发我们，若要有归结过程使由S可归结出□，就可从S的语义树T出发，说明必有两个失败结点所对应的子句做归结，将归结式放入S，就使T倒塌。重复这个过程直到语义树仅由树根组成为止。树根N0是失败结点，I(N0)＝Φ，必然是已归结出空子句□所致。
　　然而上述从语义树入手的分析，仅能说明失败结点所对应的S的两个子句的基例可做归结。归结法完备性要求说明当S不可满足时，子句间必可做归结直到得出□。于是还需解决由基例间可做归结到怎样实现子句间的可做归结的问题，也就是由常量子句可做归结导出变量子句也可做归结的问题。这一步很重要，由提升引理给出。
　　2． 提升引理
　　，是无公共变量的子句， C1'，C2'分别是，的例，而R'是 C1'，C2'的归结式，则存在，的归结式R，使得R'是R的例。
证明 证明
  （1） 依定义
　　　R' ={ C1'-{Φ'}}∪{ C2'-{～Φ' }}
　而　C1' = θ
　　　C2' = θ
　　　置换θ中的分子项为常量
（2）{Φ1,…,Φm}是中在θ下映射成Φ'的文字，即
　　　Φ1θ =…=Φmθ =Φ'
　　 {～ψ1,…,～ψn}是C2中在θ 下映射成～ψ'的文字，即
　　　～ψ1θ=… =～ψnθ=～ψ'=～Φ'
（3）令σ是{Φ1,…,Φm}的mgu
　　 Φ1σ=…=Φmσ=Φ″
　　 τ是{～ψ1,…,ψn}的mgu
　　　～ψ1τ=… =～ψnτ=～ψ″
　　作δ=σ∪τ。
（4）Φ'必是Φ″的例，ψ'必是ψ″的例
　　于是Φ″和ψ″必有合一者。
　　令r是Φ″，ψ″的mgu.
（5）有
　　　R={δ・r-{Φ1,…,Φm}δ・r}∪{δ・r-{～ψ1,…,～ψn}δ・ r}
　　　R'={θ-{Φ1,…,Φm}θ }∪{θ -{～ψ1,…,～ψn}θ}
　因　Φ'是Φ″和ψ″的例，θ不如δ・r更一般，可得
　R'必是R的例，即　R'＝Rλ

　　今以
　　　　＝P(x)∨P(y)∨～Q(z)
　　　　=～P(f(u))∨～P(f(b))∨W(v)
　　为例来说明提升引理的证明过程。
　　（1）θ＝{f(b)/x,f(b)/y,a/z,b/u,c/v}下，
　　　　C1'＝θ＝P(f(b))∨P(f(b))∨～Q(a)=P(f(b))∨～Q(a),Φ'=P(f(b))
　　　　C2' =θ=～P(f(b))∨～P(f(b))∨W(c)=～P(f(b)) ∨ W(c),～ψ'=～Φ' =～ P(f(b))。
　　　　R'＝～Q(a)∨W(c)。
　　（2）Φ1=P(x),Φ2=P(y)是中在θ下变为Φ'＝P（f(b)）的文字。
　　　　～ψ1=～P(f(u)),～ψ2=～P(f(b))是中在θ下变为～Φ'=～ψ'=～P(f(b))的文字。
　　（3）σ为{Φ1,Φm}的mgu,　∴σ＝{x/y}
　　　　Φ1σ=Φ2σ=Φ″=P(x)
　　　　τ为{～ψ1，～ψ2}的mgu ，∴τ＝{b/u}
　　　　～ψ1τ=～ψ2τ=～ψ″=P(f(b))
　　　　δ=σ∪τ={x/y,b/u}
　　（4）Φ'=P(f(b))是　Φ″＝P(x)的例。
　　　　 ψ'＝P(f(b))是　ψ″=P(f(b))的例。����
　　　　 Φ″，ψ″必可合一，有mgu　r={f(b)/x}
　　（5）R={δ・r -{Φ1,Φ2}δ・r }∪{δ・r -{～ψ1，～ψ2}δ・r }
　　　　　=～Q(z) ∨W(v)
　　　　δ・r={x/y,b/u}・{f(b)/x}={f(b)/y,b/u,f(b)/x}
　　　　R' =～Q(a)∨W(c)
　　　　R' =R・λ 其中λ ={a/z,c/v}
　　3．完备性定理
定理 定理
  　设S是不可满足的当且仅当存在一个使用归结推理规则的从S到空子句□的推理过程。
证明 证明
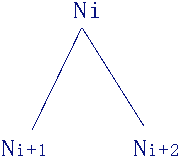  　若存在从S到□的使用归结规则的推理过程，由于两子句的归结式是这两个子句的逻辑推论，而空子句□是由形如P与～P这一对矛盾式导出的，从而S必是不可满足的。
　若S是不可满足的，则
　（1） 依Herbrand 定理必有S的有限封闭语义树T*。
　（2） T*必有形如右图的树叉，其中Ni+1,Ni+2为失败结点。
　（3） I(Ni+1),I(Ni+2)分别使S的基例C1，Cm为假。
　（4） C1，Cm 必可做归结，有归结式R'(C1,Cm)并将R'(C1,Cm)并入S。
　（5） I(Ni)或I(Nj)，Nj为Ni的父辈结点，必使R'(C1,Cm)为假。从而Ni或Nj必是S∪{R'}的语义树的失败结点，这棵封闭语义树较T*倒塌了两枝。
　（6） 重复（2）→（5）的过程，直到封闭语义树倒塌成仅由根结点N0构成为止，而N0是失败点。由于I(N0)＝φ，这时的S∪{R',…}这有限集必含有□。
　　从（1）→（6）表明了，当S是不可满足的时，必有从S到□的基例的归结过程。
　（7） 依提升引理，S不可满足，必有从S到□的归结过程。
　尚需指出有关归结法的完备性，如果所讨论的公式或子句集S中允许出现等号或不等号时，归结法就不完备了。如
　　　　P(A)∧(A＝B)→P(B)
这样简单的推理，使用归结法并不成功，原因是S中尚需表明有关等号的反身性、传递性、对称性和可替换性等公理，但这又过于繁琐了，如果在归结推理规则外，另外加入一条推理规则，即
　　　若　＝L(t1)∨C1'
　　　　　= (t1=t2)∨C2'
　　　成立，必有　L(t2)∨C1'∨C2'　成立。
　　这时的归结法是完备的了。
　　再有，若S并不是不可满足的，则使用归结法是得不到任何结果的。