第二章 归结推理方法

　　2.3.3 语义树
　　对S的不可满足性，从几何上做些讨论是有益的。可将S的所有可能的解释展示在一棵树上，进而观察每个分枝对应的S的逻辑真值是真是假，要展现S的解释于树中，自然要依S的原子集A了。
例题 例1:
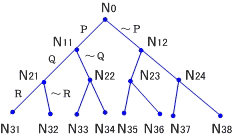
  　设子句集S的原子集
　A={P，Q，R}(属命题逻辑。这时S的原子集就是S中出现的全体原子命题)
　对A以一棵二叉树来描述，如可以N0为根结点，向下分两枝到N11，N12，分别以P和～P标记在N0N11，N0N12分枝上。再从N11，N12，向下各分两枝到N21，N22，N23，N24，分别以A中的Q和～Q来标记在各分枝上(向左的分枝标记Q，向右的分枝标记～Q)，最后从N21，N22，N23，N24再向下各分两枝到N31，…，N38，分别以A中的R和～R来标记。这棵树便称作子句集S的语义树（见图2.1）。
图示  
 

图2.1语义树
　为了方便，常以I(N)示从根结点到结点N分枝上所标记的所有文字的并集。如　　
　　　　　　I(N34)＝{P,～Q,～R}
例题 例2:
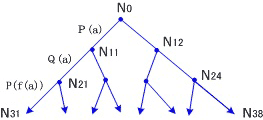
  　对子句集S＝{P(x)∨Q(y),～P(a),～Q(b)}画出相应的语义树。
　因为 H＝{a ,b}
　　　 A={P(a),Q(a),P(b)，Q(b)}
　从A出发，同例1便可画出P(a),Q(a),P(b),Q(b)构成的语义树。
　由于H一般是可数集，从而S的语义树一般是棵无限树。
例题 例3:
  　对子句集S＝{～P(x)∨Q(x),P(f(y)),～Q(f(y))}画出相应的语义树。
　因为　H＝{a ,f(a),f(f(a)), …}
　　　　A＝{P(a),Q(a),P(f(a)),Q(f(a)), …}
　从A出发便可画出S的语义树，这是棵无限树（见图2.2）。
图示  
 

图2.2　无限语义树
　S的语义树是完全的，如果对该语义树的所有叶结点N来说，I(N)包含了S的原子集A＝{,,…}中的所有元素Ai或～Ai,i=1…n…。
　　通过对S的完全语义树的观察，便可看到S的所有的解释，这棵树的每个直到叶结点的分枝都对应于S的一个解释。特别对有限树来说，若N是叶结点，那么I(N)便是S的一个解释。为讨论S的不可满足性，就可通过对语义树每个分枝来计算S的真值而实现。
　　有时并不需要无限地延伸某个分枝方能确定在相应的解释下S取假值。如果某个分枝延伸到结点N时，I(N)已使S的某一子句的某一基例为假，就无需对N再做延伸了。
　　如果结点N的I(N)使S的某一子句的某一基例为假，而N的父辈结点不能判断这个事实，就说N是失败结点。
　　如果S的完全语义树的每个分枝上都有一个失败结点，就说它是一棵封闭树。
　　就例3而言，图2.2所示的完全语义树便具有每个分枝上都有失败结点这一性质，从而是棵封闭树，如果从图2.2剪去所有失败结点以下的分枝便得相应的封闭树图2.3。
图示  
 

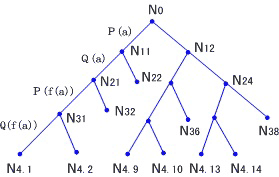图2.3封闭语义树
　　如I(N22)＝{P(a),～Q(a)}，这个S的部分解释已使S中的子句～P(x)∨Q(x)的基例～P(a)∨Q(a)为假了，而N11，N0不具有这个性质。若将I(N22)扩充为S的解释，仍然会使S为假，扩充的部分对使S为假已不起作用了。从图上看无需对N22再作延伸了。
　　再如I(N41)={P(a),Q(a),P(f(a)),Q(f(a))},它使S的子句中的子句 ～Q(f(y))的基例～Q(f(a))为假,而N41的父辈不能使S的某子句的某基例为假，从而N41是失败结点。同样，为讨论S的不可满足性无需对N41做延伸了。
　　现在已不难想像，S的不可满足性与封闭语义树的关系了。