这种模式语言语句的一个特别的语义涉及到了"可能世界"的概念。尽管在这里不对"可能世界"进行讨论,但是可以概括的说,一个智能体,只有在其所有可能的域中命题都为真时,才可以称此智能体知道这个命题。反之,如果在智能体的某个可能域中的命题为假,那么它就不知道该命题。即使没有对知识的逻辑语义的深刻认识,我们仍然可以采用一些方案,使得当前智能体可以去推理其它智能体的置信。这些方案使用了公理,它声明了带有一个新的推理规则和假言推理的知识的特殊属性。
一些常见的公理模式有。
分布公理:
[Κα(φ)∧Κα(φ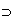 ψ)] ψ)]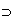 Κα(ψ)
(1) Κα(ψ)
(1)
这里"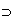 "表示逻辑蕴涵,即"→"。 "表示逻辑蕴涵,即"→"。
它要表示的意思是:如果一个智能体知道φ并且也知道φ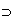 ψ(φ蕴涵ψ,或φ可以推出ψ),那么该智能体也知道ψ(因为我们假定它能执行假言推理)。这个公理模式有时可以用如下等价形式表示: ψ(φ蕴涵ψ,或φ可以推出ψ),那么该智能体也知道ψ(因为我们假定它能执行假言推理)。这个公理模式有时可以用如下等价形式表示:
Κα(φ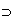 ψ) ψ)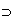 [Κα(φ) [Κα(φ)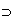 Κα(ψ)]
(2) Κα(ψ)]
(2)
这个公理被称为分布公理,因为它表示了在蕴涵的意义下对Κ算子进行分布。
知识公理:
知识公理表示一个智能体不可能知道错误的事情:
Κα(φ)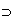 φ
(3) φ
(3)
即,如果一个智能体知道一个事实存在,则该知识存在。如果,ψ是假(矛盾式),则有Κα(F)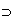 F,于是,~Κα(F) F,于是,~Κα(F)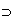 T,即~Κα(F)(α不知道F这件事是真的)。此公式说明知识公理隐含表示了:一个智能体不知道矛盾式:~Κ(α,F) T,即~Κα(F)(α不知道F这件事是真的)。此公式说明知识公理隐含表示了:一个智能体不知道矛盾式:~Κ(α,F)
肯定-自省公理:
作为知识的第三个特性,可以假定如果一个智能体知道一些事情,它就知道它知道它们。这个特性由肯定-自省公理(positive-introspection
axiom)来表示:
Κα(φ)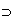 Κα(Κα(φ))
(4) Κα(Κα(φ))
(4)
否定自省公理:
同时在一些知识公理中,如果一个智能体不知道一些知识,它知道它不知道这些知识,这被称为否定内省公理,表示如下:
~Κα(φ)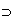 Κα(~Κα(φ))
(5) Κα(~Κα(φ))
(5)
一些常见的智能体规则有。 |