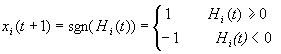
离散Hopfield神经网络(DHNN)是一个离散时间序列系统，网络结构上只有一个神经元层，各个神经元的转移函数都是线性阈值函数。每个神经元均有一个活跃值，或称之为状态（取两个可能值之一） 　　设N是一n阶神经网络。连接权重为W，状态改变阈值为θ。则N由(W,θ)唯一的定义，其中：W为n×n对称矩阵，其中wij为神经元（节点）i与j的之间的连接权值；θ为n维向量，θi表示神经元i的阈值。 　　每个节点可处于两个可能状态之一，只能取值1或－1。以xi(t)表示任意时刻t（t为正整数）节点i的状态，向量X(t)是神经网络N在t时刻的状态向量。描述状态变化的方程式可写为 　　 　　 　　整个网络的状态向量X(t)∈{-1, +1}n，如果wij = 0( i = 1, 2, 3, …n)则称为无反馈的DHNN，否则称为有自反馈的DHNN。