A1 ∧ A2 →B
CF(A1 ∧ A2 ) = min { CF(A1), CF(A2) }
2)"或"的计算:
A1 ∨ A2 →B
CF(A1 ∨ A2 ) = max { CF(A1), CF(A2) }
3)"非"的计算:
CF(~A ) = -CF(A)
4)由A, A →B,求 CF(B):
CF(B) = max(0,CF(A))・CF(B,A)
5)合成,由两条规则求出再合并:
由规则A1→B可求得CF1(B),同时又有规则A2→B,可求得CF2(B)。如何根据这两条规则的产生的结果,计算其合成后的可信度CF(B)?
先有:
CF1(B)= max(0,CF(A1))・CF(B,A1)
CF2(B)= max(0,CF(A2))・CF(B,A2)
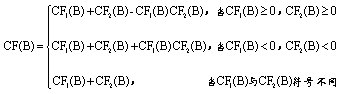
CF1(B)和CF2(B)是同时发生的,即可以是分别从两条完全独立的途径得到的知识。