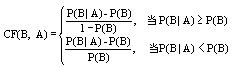
CF(B,A)表示的意义:
证据为真是相对于P(~B) = 1 - P(B)来说,A对B为真的支持程度,即A发生更支持B发生,此时 CF(B,A)≥ 0。
相对于P(B)来说,A对B为真的不支持程度。即A发生不支持B发生,此时 CF(B,A)< 0。 它总是满足条件-1 ≤ CF(B,A) ≤ 1。
CF(B, A)的特殊值:
CF(B, A) = 1, 前提真,结论必真
CF(B, A) = -1, 前提真,结论必假
CF(B, A) = 0 , 前提真假与结论无关
实际应用中CF(B, A)的值由专家确定,并不是由P(B|A), P(B)计算得到的。同时还要注意的是,CF(B,A)表示的是增量P(B|A)-P(B)对1-P(B)或P(B)的比值,而不是绝对量的比值。