21，单位耗散:
如果一个问题，任意一个节点与它的后继节点之间的耗散值都为1，则称该问题是单位耗散的。

22，深度优先搜索:
一种盲目搜索方法，该方法每次选择深度最深的节点优先进行搜索。

23，宽度优先搜索:
一种盲目搜索方法，该方法每次选择深度最浅的节点优先进行搜索。当问题有解时，宽度优先搜索方法一定能找到问题的解。当问题为单位耗散时，宽度优先搜索一定能找到问题的最优解。

24，A算法:
一种启发式搜索方法。该方法对节点n，定义评价函数： f(n)=g(n)+h(n) 对OPEN表中的元素按照f值，从小到大进行排列，每次从OPEN表中取出f值最小的节点扩展，这种图搜索算法成为A算法。

25，A*算法:
如果对于任何节点n，有h(n)≤h*(n)，则此时的A算法称为A*算法。

26，旅行商问题（TSP问题）:
一个推销员要到n个城市去办理业务，城市间里程数已知，如何从某个城市出发，每个城市只允许访问一次，并且必须访问一次，最后又回到原来的城市，怎么走才能使得所行走的路线路程最短。该问题称为旅行商问题，简称为TSP问题。

27，可采纳性:
如果一种搜索算法，当问题有解时一定能找到问题的最优解，则称该算法是可采纳的，或者说该算法具有可采纳性。

28，扩展的节点数:
在求解一个问题中所扩展的节点的总数，称为扩展的节点数。一个节点无论被重复扩展了多少次，在计算扩展的节点数时，都只计算一次。

29，单调限制条件:
一个启发函数h，如果对所有节点和（是的子节点），都有h() - h()≤C(，)且h()＝0，其中是目标节点，则称该h函数满足单调限制条件。

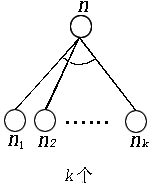
30，k-连接符:
在与或图中，一个节点与它的k个与子节点间用下图的形式连接，称为k－连接符。

31，解图:
与普通图的解路径相对应，与或图的解用解图表示。解图的求法是：从节点n开始，正确选择一个外向连接符，再从该连接符所指的每一个后继节点出发，继续选一个外向连接符，如此进行下去直到由此产生的每一个后继节点成为目标节点集合N中的一个元素为止。

32，局部图的耗散值:
局部图的耗散值定义如下： ①若n是局部图的一个叶节点，则k（n，N）＝h(n)； ②若n由一个外向连接符指向后继节点{n1，…，ni}，并设该连接符的耗散值为Cn，则 k（n，N）＝Cn+ k（n1，N） + … + k（ni，N） 其中，h(n)表示节点n到目标节点集的最佳解图耗散值的估计。

33，解图的耗散值:
解图的耗散值定义如下： ①若n是N的一个元素，则k（n，N）＝0； ②若n由一个外向连接符指向后继节点{n1，…，ni}，并设该连接符的耗散值为Cn，则 k（n，N）＝Cn+ k（n1，N） + … + k（ni，N） 其中N为目标节点的集合。

34，能解节点:
能解节点定义如下： ①终节点是能解节点； ②若非终节点有"或"子节点时，当且仅当其子节点至少有一能解，该非终节点才能解； ③若非终节点有"与"子节点时，当且仅当其子节点均能解，该非终节点才能解。

35，不能解节点:
不能解节点定义如下： ①没有后裔的非终节点是不能解节点； ②若非终节点�"或"子节点时，当且仅当所有子节点均不能解时，该非终节点才不能解； ③若非终节点有"与"子节点时，当至少有一子节点不能解时，该非终节点才不能解。

36，最佳解图（最优解图）:
耗散值最小的解图称为最佳解图。

37，AO*算法:
AO*算法是一种用于对与或图进行搜索的启发式搜索算法，该算法对目前找到的局部图进行评价，选择耗散值最小的局部图进行优先搜索，直到找到一个解图为止。当启发函数h满足单调条件时，在问题有解的情况下，AO*算法一定能找到最佳解图结束。

38，博弈树搜索:
对双人博弈问题的一种启发式搜索方法。搜索的目的是寻找当前棋局下的最佳走步。博弈树搜索是一类特殊的与或图搜索，主要有极小极大搜索和α－β剪枝法等。

39，Grundy博弈（分钱币问题）:
Grundy博弈是一个分钱币的游戏。有一堆数目为N的钱币，由两位选手轮流进行分堆，要求每个选手每次只把其中某一堆分成数目不等的两小堆。如此进行下去直到有一位选手先无法把钱币再分成不相等的两堆时认输为止。

40，α剪枝:
在博弈树搜索中，若任一极小值层节点的β值小于或等于它任一先辈极大值居节点的α值，即α（先辈层）≥β（后继层），则可中止该极小值层中这个MIN节点以下的搜索过程。这个MIN节点最终的倒推值就确定为这个β值。