（2）建立规则连接图结构

当一个问题确定以后，规则之间的连接关系就确定了。如果事先就"画"好这些连接关系，就可以在求解问题时直接使用了，从而提高系统的求解效率。这种方法相当于将几个规则联合成为一个"大"规则，在需要时一起使用。除了要保留规则间的连接关系外，还要同时保留规则间匹配时产生的所有置换，在实际使用时，还要判断这些置换是否是一致的。因为和具体的子目标匹配后，可能会导致置换的不一致性。

这个方法是预先计算规则间所有可能的匹配，组成规则连接图，并存储产生的各个置换，在求解具体问题时再调用这些结果。只要规则集不变，这些结果对所有具体问题都有效，当然只有对不太大的规则集来说，这个方法才是实际的。

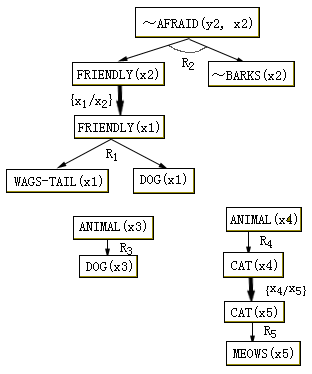
图4.30 一个规则连接图

　　图4.30是用前面猫和狗例题的规则集构造的规则连接图。构造的办法是先把每条规则的与或图表示画好，然后把一条规则前项的某一个文字通过匹配弧与另一条规则的后项文字连接起来，并在匹配弧上标上mgu。
　　当要求解一个实际问题时，把目标与或图中的各个文字节点连接到某一条规则后项的文字上（对应的文字能匹配），把各个事实节点连接到某一条规则前项的文字上（对应的文字能匹配），这样就实现了目标节点和事实节点同规则连接图相结合的扩大连接图。接着就寻找其中的一个候选解图，一旦找到候选者，就计算其置换集的合一复合。若存在，就找到一个一致解图，从而得到问题的解，否则就必须再查找该连接图另外的候选解图。
　　这种方法实际上根据预先计算的连接图结构，不断地产生愈来愈大的一系列与或图。一个很复杂的问题是可能要在候选解图中多次使用同一条规则的连接图，每次使用时变量都要改名，因而这些改名变量也必须出现在候选解图的置换之中。下面举一个特殊的例子来说明多次使用规则连接图的复杂性。

　　这是一个多次使用同一个规则的例子。当多次使用同一规则时，需要对规则中的变量进行换名，使得规则在不同的使用处，其变量名是不相同的。这一点是必须要注意的，否则可能会导致解图的不一致性，从而导致得不到问题的解。

　　设有规则P（x）→P（f（x））和事实P（A），要证明目标公式P（f（f（A）））。这个问题的规则连接图如图4.31所示，图中有一个规则前项和后项的匹配弧，但未加置换标记，以便引起注意该规则的某一个新例能使其后项和原始的前项匹配等等。当目标节点、事实节点和规则连接图连结时，可得连接如图4.32所示。根据这个连接图，若两次使用这条规则（即沿匹配弧循环一次），则可得一个如图4.33所示的候选解图。由于两次使用同一条规则，因而规则中变量和连接匹配弧的转换变量都必须改名。根据图4.33中匹配置换集可求得合一复合置换为{f（A）/x，A/y}，所以这个解图是一致解图。

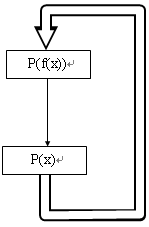
图4.31 例子的规则连接图

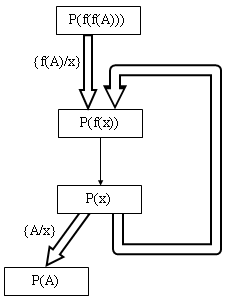
图4.32 一个连接图

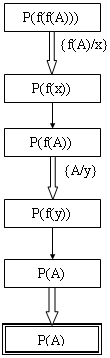
图4.33 一个候选解图