3．演绎系统的搜索策略

　　无论是正向系统还是逆向系统，其目标都是从众多的解图中，找一个一致解图。在前面的介绍中，都是在寻找完所有解图之后，再判断解图的一致性。如果在寻找解图的过程中，就判断局部解图的一致性，对于不一致的部分进行修剪，显然会提高系统求解的效率。

　　演绎系统的搜索目标是找一个一致解图，其搜索策略的基本思想是首先找一个任意解图，再检验其一致性，看是否是一致解图。如果这个候选解图不一致，则继续搜索直到找到一个一致解图为止。下面介绍两种逆向系统的搜索方法，但其思想也可用于正向系统的搜索过程。

　　（1）修剪不一致的局部候选解图

　　在扩展局部的候选解图前，就进行一致性的检验，若能及时发现不一致的局部候选者并立即修剪掉，则将减少无用的搜索，致使效率提高。下面通过两个例子来说明这一问题。

在例1中，置换{A/x}与{B/x}是不一致的，只能保留一个。如果子目标Q(x)只有一个唯一的匹配Q(A)，则保留该匹配，而舍弃P(x)与规则R2的匹配。

例1：设要证明的目标：P（x）∧Q（x）
规则：R1：R（y）→P（y）
R2：S（z）→P（B）
事实：R（A）∧Q（A）

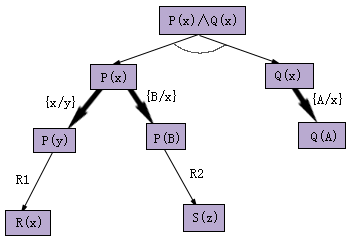
图4.28 例1的与或图

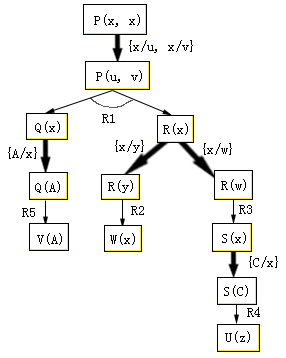
图4.29 例2的与或图

　　图4.28是已生成的一个与或图，其中包含两个局部的候选解图，这两个候选者所对应的匹配置换集分别为{{x/y}，{A/x}}和{{B/x}，{A/x}}，显然后者是不一致置换。如果Q（A）是子目标Q（x）的唯一匹配，则R2就不可能是任意一个解的一部分，因此必须中止R2以下部分的搜索，即不必要再生成S（z）的一些子目标。

　　在例2中，规则R4和R5的应用产生了两个不一致的置换{A/x}和{C/x}。对于S(x)来说，虽然规则R4是它的唯一匹配，但由于前面R(x)存在R2和R3两个匹配，而R5是Q(x)的唯一匹配，所以只能舍弃规则R4这一边的匹配，而保留规则R5这边的匹配。

例2：
目标：P（x，x）
规则：R1：（Q（u）∧R（v））→P（u，v）
R2：W（y）→R（y）
R3：S（w）→R（w）
R4：U（z）→S（C）
R5：V（A）→Q（A）
　　设演绎生成的部分与或图如图4.29所示，其中一个应用了R4和R5的局部解图是不一致的，有两个置换{A/x}和{C/x}是不一致的。如果R5对子目标Q（x）是唯一的匹配，则应修剪掉子目标U（z），而子目标S（x）仍保留并允许作置换{A/x}。