4.8 基于规则的逆向演绎系统

逆向演绎系统中，是从目标表达式出发，反方向使用规则（B规则）对目标表达式的与或图进行变换，最后得到含有事实节点的一致解图。整个推理过程的思路类同于正向系统，但具体的处理过程有其特点，本节主要介绍逆向系统的限制条件及处理方法。

　　1．目标表达式的与或形表示
　　在基于规则的逆向系统中，同正向系统一样，要用对偶形式对目标表达式进行Skolem化。即消去全称量词，对受全称量词约束的变量用Skolem函数或者常量代替，省略存在量词，所有变量默认为受存在量词约束，并进行变量换名，使得目标公式的主析取元之间具有不同的变量名。对于为什么用对偶形式对目标表达式进行变换，可以这样认为：在归结法中，是对目标表达式取否定后再进行变换，而在逆向系统中是直接对目标表达式进行变换，由于取否定后，存在量词变为全称量词，全称量词变为存在量词，所以用对偶形式直接对目标表达式进行Skolem化，与对目标的否定进行普通的Skolem化是一致的。
　　在用与或图表示目标表达式时，规定子表达式间的析取用1－连接符连接，即表示为"或"的关系，而子表达式的合取用k－连接符连接，即表示为"与"的关系。也就是说，目标表达式中的"与""或"关系，和与或图中的"与""或"关系是一致的。这与正向系统中对事实表达式的与或图表示是不一样的。这一点可以这样来理解：对于目标来说，两个子表达式间如果是析取的话，则表示只要其中一个成立则目标成立，因此在与或图中用"或"关系表示；如果子表达式间是合取的话，则必须每一个子表达式都成立，目标才能成立，所以在与或图中用"与"关系表示。
图4.26给出了一个目标表达式用与或图表示的例子。从该图的解图中，同样可以得到以下几个子句：
~P（f（z））
Q（f（y），y）∧~R（f（y））
Q（f（y），y）∧~S（y）
容易验证，这些子句刚好是该目标表达式的析取范式中的几个子句。

　　逆向系统能处理任意形式的目标表达式，在把任意目标公式化简为与或形的表示时，要使用与正向系统中对事实表达式处理方法的对偶形式。即要用存在量词量化变量的Skolem函数来替代全称量词的变量，消去全称量词，省略掉存在量词，并进行变量换名使主析取元之间具有不同的变量名。对化简得到的与或形表达式，用与或图表示时，规定子表达式间的析取关系用1－连接符来连接，表示成或的关系，而子表达式间的合取关系则用k－连接符来连接，表示成与的关系。下面给出一个例子的化简结果及其与或图的表示。

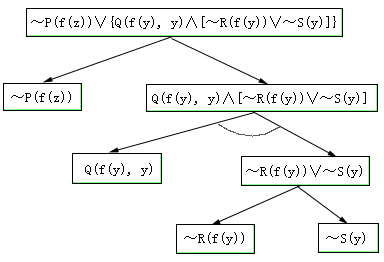
图4.26目标公式的与或图表示

例：目标公式：（ y）（ x）（P（x）→（Q（x， y）∧~（R（x）∧S（y））））
Skolem化后：~P（f（y））∨（Q（f（y）， y）∧（~R（f（y））∨~S（y）））
变量标准化：~P（f（z））∨（Q（f（y）， y）∧（~R（f（y））∨~S（y）））
这个目标的与或图表示如图4.26，其子句集可以从结束在端节点的解图集中读得：
~P（f（z））
Q（f（y），y）∧~R（f（y））
Q（f（y），y）∧~S（y）
　　这里规定子句是文字的合取式，而这些子句的析取式是目标公式的子句形式（析取范式）。目标公式的与或图中，根节点的任一后裔都称为一个子目标节点，其中的表达式称为子目标。