前面讲解了谓词逻辑情况下，如何用一个规则对与或树进行变换，以及如何判断一个解图是否是一致的。下面的例子说明了基于规则的正向演绎系统的全部过程。
在该例子中，规则1用自然语言表示为："All terriers are dogs"。该规则用谓词逻辑可以表示为：
TERRIER（x）→DOG（x）
也可以表示为：
~DOG（x）→~TERRIER（x）
这里用的是第二种表达方式，其原因是该问题的目标是：
~TERRIER（z）∨NOISY（z）
在进行规则变换时，需要用到~TERRIER（x）。由此可见，在用基于规则的正向系统求解问题时，需要根据问题的特点，变换不同的表达方式。而在归结方法中，则不需要考虑这样的问题。

最后再举一个简单的例子来说明正向产生式系统的演绎过程。
设事实和规则描述如下：
Fido barks and bites， or Fido is not a dog.
F：~DOG（FIDO）∨（BARKS（FIDO）∧BITES（FIDO））
All terriers are dogs.
R1：~DOG（x）→~TERRIER（x）
Anyone who barks is noisy.
R2：BARKS（y）→NOISY（y）

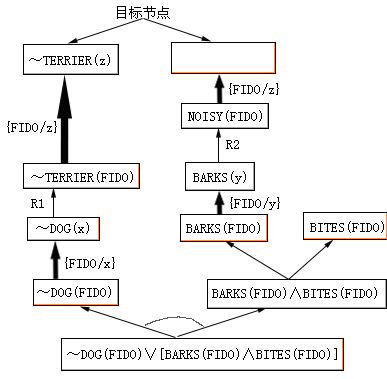
图4.25 猎犬问题的与或图

要证明的目标是
There exists someone who is not a terriers or who is noisy.
目标公式： ~TERRIER（z）∨NOISY（z）
公式中x、y是全称量词量化的变量，而z是存在量词量化的变量。图4.25给出演绎得到的与或图，图中结束在目标节点的一个一致解图，有置换集{{FIDO/x}，{FIDO/y}，{FIDO/z}}，它的合一复合是u＝{ FIDO/x，FIDO/y，FIDO/z}。根据这个一致解图，目标公式 ~TERRIER（z）∨NOISY（z）是事实和规则的逻辑推论，因而得到了证明。如果用这个合一复合u应用于这个目标公式，可得
~TERRIER（FIDO）∨NOISY（FIDO）
它是已证目标公式的例，可作为一个回答语句。关于求解一致解图的搜索策略等问题，将留待下一节讨论。