图4.24是这个例子应用规则变换后得到的与或图，它有两个解图，对应的两个子句是
　　S（A）∨X（B）∨Q（A， A）
　　S（A）∨X（B）∨R（B， B）
　　它们正是事实和规则公式组成的子句集对文字P进行归结时得到的归结式。

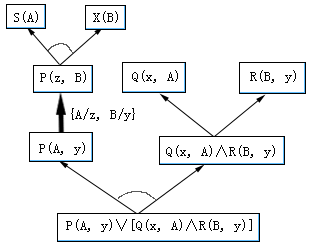
图4.24应用一条含有变量的规则后得到的与或图

　　一个解图是否是一致的，需要看该解图所涉及的若干个置换组成的置换集是否存在矛盾。当置换集没有矛盾存在时，称该置换集是一致的，也就是没有矛盾的，否则就是不一致的。只有当解图所涉及的置换集是一致的时，解图才是一致的。置换集一致的充分必要条件是该置换集存在合一复合。置换集的合一复合也是一个置换，表示的是置换集中所有置换"综合"以后的结果。
　　求一个置换集的合一复合，首先构造U1、U2两个表达式，其中U1由置换集中的所有被置换的变量组成，U2由与U1中的变量所对应的置换项组成。当U1、U2可以合一时，则所对应的置换集是一致的（一致置换），它们的mgu就是该置换集的合一复合。
　　合一复合是可结合、可交换的。这是一个很好的性质，说明在用基于规则的正向演绎方法求解问题时，与使用规则的次序无关。

　　当一个与或图应用了好几条规则之后，推出的与或图将含有多个的匹配弧，这时任一解图可能有多于一个的匹配弧（对应的置换是u1，u2，…），因此在列写解图的子句集时，只考虑具有一致的匹配弧置换的那些解图（一致解图）。一个一致解图表示的子句是对得到的文字析取式应用一个合一复合的置换之后所得到的子句。
置换的一致集和置换的合一复合这两个概念定义如下。设有一个置换集{u1，u2，…，un}，其中是置换对集合，t是项，v是变量。
根据这个置换集，再定义两个表达式：

置换（u1，…，un）称为一致的，当且仅当U1和U2是可合一的。（u1，…，un）的合一复合（unifying composition）u是U1和U2的最一般的合一者。下面给出几个合一复合结果的实例。

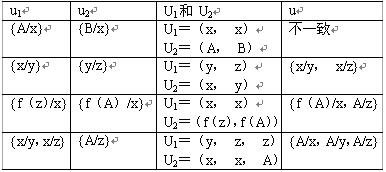
　　可以证明对一个置换集求合一复合的运算是可结合和可交换的（求置换的合成是不可交换的），因此一个解图对应的合一复合不依赖于构造这个解图时所产生的匹配弧的次序。再强调一下，我们要求一个解图具有一个一致匹配弧的置换集，这样该解图所对应的子句才是从初始事实表达式和规则公式集推出的子句。
　　有些时候演绎过程会多次调用同一条规则，这时要注意每次应用都要使用改名的变量，以免匹配过程产生一些不必要的约束。此外，也可多次使用同一目标文字来建立多个目标节点，这也要采用改名的变量。