（2）谓词逻辑的情况

　　对于谓词逻辑，除了像前面介绍的那样，要对事实和规则进行处理外，与命题逻辑最大的差别是在匹配时需要进行合一，而且还要检查同一个解图中的合一置换是否是一致的。所谓的一致置换，是指这些置换是没有矛盾的。一个具有一致置换的解图称为一致解图。非一致的解图是没有意义的。
　　对于目标表达式，用对偶形式进行Skolem化，即消去全称量词，对受全称量词约束的变量用Skolem函数或者常量代替，省略存在量词，所有变量默认为受存在量词约束，并进行变量换名，使得目标公式的主析取元之间具有不同的变量名。对于为什么用对偶形式对目标表达式进行变换，可以这样理解：在归结法中，是对目标表达式取否定后再进行变换，而在逆向系统中是直接对目标表达式进行变换，由于取否定后，存在量词变为全称量词，全称量词变为存在量词，所以用对偶形式直接对目标表达式进行Skolem化，与对目标的否定进行通常的Skolem化是一致的。

　　在谓词逻辑的情况下，对事实表达式和规则蕴涵式的处理过程在本节一开头已经进行了讨论，下面主要是讨论对含有存在量化变量或全称量化变量的目标公式应如何处理，以及规则应用时的匹配问题。
　　对具有量词量化变量的目标公式来说，化简时所使用的Skolem化过程是前面讨论过的事实和规则所用的Skolem化过程的对偶形式。即目标中属于存在量词辖域内的全称量化变量要用存在量化变量的Skolem函数来替代，经过Skolem化的公式只剩下存在量词，然后对析取元作变量改名，最后再把存在量词省略掉。
例如，设目标公式为
（y）（x）（P（x， y）∨Q（x， y））
用Skolem函数消去全称量词后有
（y）（P（f（y）， y）∨Q（f（y）， y））
和命题逻辑的情况一样，目标公式也限制为文字的析取式，这时要进行变量改名，使每个析取元具有不同的变量符号，于是有
（y）P（f（y）， y）∨（y1）Q（f（y1）， y1）
以后目标公式中的变量都假定受存在量词的束约。
　　现在再来看一下应用一条规则L→W对与或图进行变换的过程。设与或图中有一个端节点的文字L′和L可合一，mgu是u，则这条规则可应用，这时用匹配弧连接的后裔节点是L，它是规则后项Wu对应的与或图表示的根节点，在匹配弧上标记有u，表示用u置换后可与规则匹配。

　　在该例中，P(x, y)与P(A, B)进行合一，置换是{A/x, B/y}，将规则P（A，B）→（S（A）∨X（B））连接到图中，得到图4.24所示的与或图。刚好该规则不含有变量，如果含有变量的话，对规则的结论部分，要同时施予该置换。值得注意的是，图中的匹配弧（图中的空心粗箭头）只是表示两个谓词匹配，其箭头并没有指示出置换的"方向"，应完全按照合一置换的原则进行。比如，如果该例改写为：
　　事实与或形表示 P（A，y）∨（Q（x，A）∧R（B，y））
　　规则蕴涵式 P（z，B）→（S（z）∨X（B））
　　则施以规则后的与或图如下图所示。

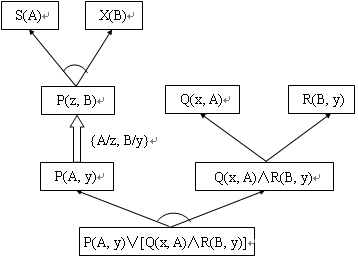
　　图中，P(A, y)与P(z, B)进行合一，置换为{A/z, B/y}，该置换作用于规则中，使得S(z)变为S(A)。由于要表示出参予合一的原始谓词，所以对规则的置换只作用于规则的结论部分，规则的前提部分，还保留变量，这样可以看的更清楚一些。
例：事实与或形表示 P（x， y）∨（Q（x， A）∧R（B， y））
规则蕴涵式 P（A， B）→（S（A）∨X（B））