这个应用一条规则之后演绎得到的新与或图，可以认为即可表示原始事实，又能表示推出的事实表达式。如果撇开匹配弧后面的部分，那么就可以从初始与或图的4个解图中，得到对应的4个子句组成的子句集：
S∨（P∨Q）
S∨R
（T∨U）∨（P∨Q）
（T∨U）∨R
如果把新得到的与或图，其匹配弧看成是1-连接符，则可从解图集中得到6个子句的子句集：
X∨Z∨P∨Q
X∨Z∨R
Y∨Z∨P∨Q
Y∨Z∨R
（T∨U）∨（P∨Q）
（T∨U）∨R
　　可以看出前面4个新增加的子句就是初始事实和规则表示的子句一起组成的子句集进行归结可能得到的所有归结式，即演绎得到的子句集就是归结式的完备集。
下面说明一下这个结论。
把规则化成子句表示后可得两个子句
~S∨X∨Z
~S∨Y∨Z
于是基本子句集为
{S∨（P∨Q）， S∨R， （T∨U）∨（P∨Q）， （T∨U）∨R， ~S∨X∨Z， ~S∨Y∨Z}
　　不难求得所有的4个归结式正好就是解图集读到的4个新子句。也就是说一条规则的应用结果，就得到归结式的完备集，即这条规则的应用演绎出所有的逻辑推论来。
　　一个基于规则的正向演绎系统，其演绎过程就是不断地调用匹配上的规则对与或图进行变换，直到生成的与或图含有目标表达式为止，也就是要用目标公式作为系统的结束条件。正向系统的目标表达式要限制为文字析取形（子句形）的一类公式，当目标公式中有一个文字同与或图中某一个端节点所标记的文字匹配上时，和规则匹配时做法一样，通过匹配弧把目标文字添加到图上，这个匹配弧的后裔节点称为目标节点。这样当产生式系统演绎得到的与或图包含有目标节点的解图时，系统结束演绎，这时便推出了一个与目标有关的子句。
下面的简例说明系统的推理过程。

　　在该例中，经过两次规则变换后，得到如图4.23所示的与或图。其中一个解图的叶节点是C和G，分别与目标表达式C∨G中的文字C和G匹配，说明目标C∨G是该问题的逻辑推论，从而证明目标公式成立。
　　值得注意的是，只要求解图的叶节点全部与目标公式中的文字匹配上，并不要求目标公式中的每一个文字都必须与解图中的一个叶节点匹配。以该例为例，即便是目标公式变为C∨G∨P∨Q，同样也可以推出目标公式成立，因为已经逻辑推导出C∨G成立。C∨G∨P∨Q只是在C∨G上又"或"上了两个命题，如果C∨G成立，C∨G∨P∨Q当然也成立。

例：事实表达式：A∨B
规则集：A→C∧D
B→E∧G
目标公式：C∨G

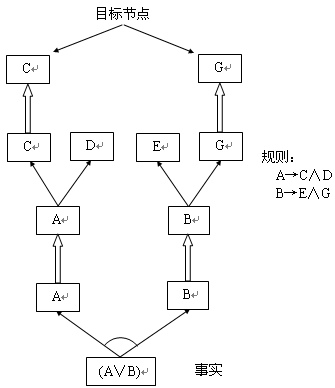
图4.23满足结束条件的与或图

　　应用完这两条规则之后，得到的与或图如图4.23所示，其中有一个解图是满足目标公式（C∨G）所建立的结束条件。可以看出这种产生式系统具有可交换的性质，因而可以使用不可撤回的控制策略求出解图。