2．应用规则对与或图作变换

　　正向产生式系统是以正向方式使用规则（F规则）对表示综合数据库的与或图结构进行变换，这些规则是以蕴涵形给出，在讨论应用它们进行推理之前，对规则形式的限制作一点说明。
　　为了讨论问题简单起见，设规则的左侧具有单文字的形式，即L→W，其中L是单文字，W是任一化成与或形的公式。这个蕴涵式中的所有变量都假定有全称量词的约束，并且变量已经换名，使之与事实公式或其他规则公式中的变量区别开来。为了得到这种可应用的形式，对原始蕴涵式必须作必要的化简。设原始公式为
（x）（（（y）（z）P（x，y，z））→（u）Q（x，u））
则化简步骤如下：
（1）暂时消去蕴涵符号
（x）（~（（y）（z）P（x，y，z））∨（u）Q（x，u））
（2）处理否定符号使其作用辖域仅限于单个文字
（x）（（y）（z）（~P（x，y，z））∨（u）Q（x，u））
（3）Skolem化
（x）（（y）（~P（x，y，f（x，y）））∨（u）Q（x，u））
（4）化成前束式并隐略去全部全称量词
~P（x，y，f（x，y））∨Q（x，u）
（5）恢复蕴涵式表示
P（x，y，f（x，y））→Q（x，u）
　　对规则作单文字前项的限制将大大简化了应用时的匹配过程，对非单文字前项的情况，若形式为（L1∨L2）→W，则可化成与其等价的两个规则L1→W与L2→W进行处理。单文字的限制对实际问题的应用范围有所限制，但对演绎方法本身并不产生影响。下面分两种情况来讨论演绎的过程。
　　（1）命题逻辑的情况

　　首先以命题逻辑为例，说明如何利用规则对事实的与或图进行变换。
在一个正向演绎系统中，规则具有形式：L→W，其中L是单文字，W是与或形。它表示由L可以推导处W。如果在与或图中有一个叶节点刚好与L匹配，则可以使用规则对与或图进行变换。其方法是，将该叶节点与L用一个匹配弧连接起来，将W添加到与或图中。如图4.22所示。这样，就对与或图用规则实施了一次变换，得到了一个"更新"了的与或图。
与事实的与或图相对比，从更新后的与或图中可以得到4个新的子句：
X∨Z∨P∨Q
X∨Z∨R
Y∨Z∨P∨Q
Y∨Z∨R
　　如果将事实和规则都转化为子句的话，容易验证，这四个子句刚好是该规则所对应的子句参与归结所得到的4个归结式。从而说明，这种规则变换与归结具有一定的联系。
　　基于规则的正向演绎系统，就是不断的对与或图施以规则变换，直到找到一个解图，该解图中的所有叶节点全部都与目标公式中的文字匹配为止。

由于所有公式都不含有变量，因此应用规则的匹配过程比较简单。设初始综合数据库的与或形表达式为
（（P∨Q）∧R）∨（S∧（T∨U））
规则为
S→（X∧Y）∨Z
　　把初始数据库用与或图表示，图中有一个端节点是文字S，它正好与规则前项的文字S完全匹配，由此可直接用这条规则对与或图进行变换，即把规则后项的与或形公式用与或图表示后添加到初始数据库上，并用一个匹配弧连接起来，规则匹配后演绎的结果如图4.22所示（把根节点画在底部）。图中匹配弧后面是规则部分，其前项可看成匹配弧的一个后裔节点，由匹配上的文字标记，它表示成规则后项与或图结构的根节点。

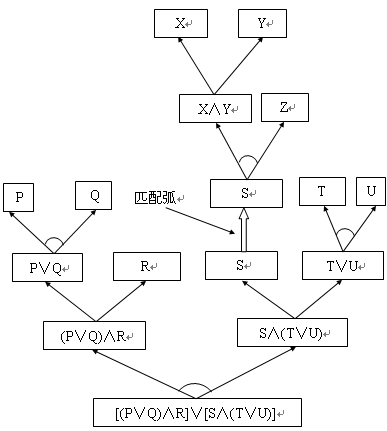
图4.22 应用一条规则后的与或图