4.7 基于规则的正向演绎系统

　　 在人工智能系统中，谓词逻辑公式常可用来表示各种知识，通常很多应用知识是用蕴涵形式直接表达，因此都带有超逻辑的或启发式的控制信息。在归结反演证明系统中，要把这些表达式化成子句表示，这就可能丢失掉包含在蕴涵形中有用的控制信息，例如下面的几个蕴涵式
~A∧~B→C， ~A∧~C→B， ~B∧~C→A，
~A→B∨C， ~B→A∨C， ~C→A∨B
　　其中任意一个式子在逻辑上都与子句（A∨B∨C）等价，而每种形式表达的蕴涵式都有其内在含有的各不相同的超逻辑的控制信息，子句形表示只给出了谓词间的逻辑关系。因此有时候会希望系统能按近于原始给定的描述形式来使用这些公式，不把它们都化成子句集，这就是基于规则演绎系统的基本思想。
　　一般情况下，表述有关问题的知识分两类：规则和事实。规则公式由蕴涵形给出的若干语句组成，是表示某一特定领域中的一般知识，并可以当作产生式规则来使用。事实公式则不以蕴涵形给出，是表示该问题领域的专门知识。本节讨论的演绎系统就是根据这些事实和规则来证明一个目标公式，这种定理证明系统是直接法的证明系统而不是反演系统。一个直接系统不一定比反演系统更有效，但其演绎过程容易为人们所理解。这类系统主要强调使用规则进行演绎，故称为基于规则的演绎系统。

1．事实表达式的与或形式及其表示

　　在一个基于规则的正向演绎系统中，首先要将事实表达式表示为"与或形"。化与或形的方法与化公式为子句集的方法有些类似，其过程如下：（1）首先按照与化子句集相类似的方法，将否定符号只作用于原子公式，所有的量词均移动到公式的左边。（2）消去存在量词，对受存在量词约束的变量进行Skolem化。即根据存在量词前面是否有全称量词约束，用常量或者函数代替受存在量词约束的变量。（3）对变量进行换名，使得不同的主合取元，具有不同的变量名。所谓的主合取元，指的是公式中用最外层的"∧"号分割开的部分。如在公式（v）（Q（v，u）∧~（（R（v）∨P（v））∧S（u，v）））中，Q（v，u）是一个主合取元，（R（v）∨P（v））∧S（u，v）是另一个主合取元。变量换名后，这两个主合取元不能有相同的变量名。（4）隐去全称量词，默认公式中的变量受全称量词约束。这样就得到了原公式的与或形。与子句集比起来，与或形更多的保留了公式的原始形式。

对一个正向演绎系统而言，事实表达式是其前提条件，是作为初始数据库描述的。这些事实化简只变换成不具蕴涵形式的与或形表示，不必完全化简为子句形，例如有事实表达式
（u）（v）（Q（v，u）∧~（（R（v）∨P（v））∧S（u，v）））
把它化成为
Q（v， A）∧（（~R（v）∧~P（v））∨~S（A，v））
再将变量进行换名，使不同的主合取元具有不同的变量名，改名后有
Q（w， A）∧（（~R（v）∧~P（v））∨~S（A，v））
这就是与或形的表示，在第二个合取元中，没有再加以展开成为范式，因此这种表示不是子句形，它与化简前的原始表达式更接近一些。
一种与或图形式可用来表示这个与或形表达式，图中每一个节点代表其中一个子表达式，子表达式间的与、或关系规定如下：

在将一个与或形用与或图表示时，其"与"和"或"的关系是刚好相反的。在与或形中的"∧"号在与或图中表达为"或"的关系，而与或形中的"∨"号，在与或图中表达为"与"的关系。可以这样来理解这个问题：与或形表达的是一个事实，其逻辑值应该为"真"。对于与或形中用符号"∧"连接的部分，其逻辑值如果为真的话，其每一子部分单独也必须为真。因此在与或图中可以表示为"或"，表示每一子部分是独立的。而对于与或形中用符号"∨"连接的部分，其逻辑值如果为真的话，并不说明其每一子部分也必须为真。只有它们"共同"在一起才为真，这些子部分之间是相互关联的。因此在与或图中用k－连接符表示为"与"。图4.21给出了一个与或形表示为与或图的例子。找出该与或图的所有解图，可以得到这样三个子句：Q（w，A），~R（v）∨~S（A，v），~P（v）∨~S（A，v），容易验证，这三个子句的集合刚好是该与或形的子句集。从这里也可以看出采用这种与或图表示方法的道理。

当母表达式为时，则每一个子表达式Ei被表示成一个后继节点，并由一个k-连接符来连接，即表示成与关系；当母表达式为时，则每一个子表达式均由1-连接符连接，即表示成或关系。

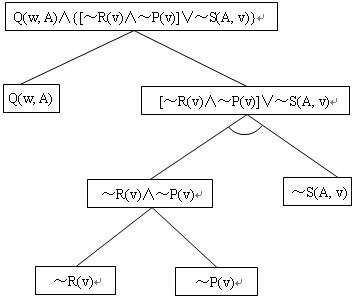
图4.21一事实表达式的一棵与或树表示

　　这样与或图的根节点就是整个事实表达式，端节点都是表达式中的每一个文字，图4.21就是上式的与或图表示。
　　有了与或图的表示，就可以求出其解图（结束在文字节点上的子图）集，我们就可以发现解图集与子句集有一一对应关系，即可从一个解图读得一个子句，这样可得对应的三个子句为：
Q（w， A）， ~R（v）∨~S（A， v）， ~P（v）∨~S（A， v）
这个性质很有用，因此也可以把这种与或图看成是子句集的一种表示。
由于与或图表示中，合取元没有进一步展开，因此变量改名受到一定的限制，这一点是不如子句集表示灵活，所以一般性差一些。
应当指出，这里的与或图是作为综合数据库的一种表示，其中变量受全称量词的约束。而在可分解产生工系统中，所描述的与或图是搜索过程的一种表示，两者有不同的目的和含义，因此在应用时应加以区别。