4.6 基于归结的问题求解方法

　　前面两章，我们介绍了一般产生式系统的图搜索策略和可分解产生式系统的与或图搜索策略这两种问题求解的方法，我们可以用谓词演算的合式公式对问题进行描述，并通过某种搜索策略求得问题的解。这一节将讨论通过谓词演算的定理证明系统进行问题求解，我们用猴子摘香蕉这个经典的例子来说明这个方法。
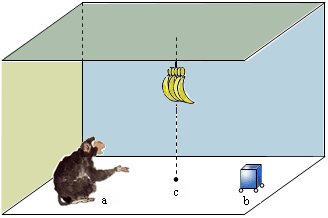
在天花板上吊有一串香蕉的房间里，有一个可移动的箱子，问一只猴子如何规划自己的行动使得能摘到香蕉，图4.19给出这个问题的示意图。

图4.19 猴子摘香蕉问题

首先用谓词逻辑的公式对问题进行描述。初始状态可表示为

三个谓词的含义是：当猴子在箱顶上时，ONBOX取真；当猴子拿到香蕉时，HB取真；谓词AT（y， x）当y处于x位置时取真。
目标状态为HB。
猴子的行为可用4个规则（算子或操作）表示，每条规则的描述形式均用谓词演算的公式组表示，P部分是前提条件，即规则的可应用条件，D是规则应用后，应从状态中删去部分，A则是加添部分。规则具体描述如下：
goto（u）
P：~ONBOX∧（x）AT（monkey，x）
D：AT（monkey，x）
A：AT（monkey，u）
pushbox（v）
P：~ONBOX∧（x）AT（monkey，x）∧AT（box，x）
D：AT（monkey，x）
AT（box，x）
A：AT（monkey，v）
AT（box，v）
climbbox
P：~ONBOX∧（x）（AT（monkey，x）∧AT（box，x））
D：~ONBOX
A：ONBOX
grasp
P：ONBOX∧AT（box，c）
D：~HB
A：HB
以这些描述为基础，就可用状态空间法进行求解。