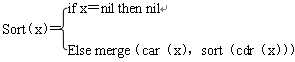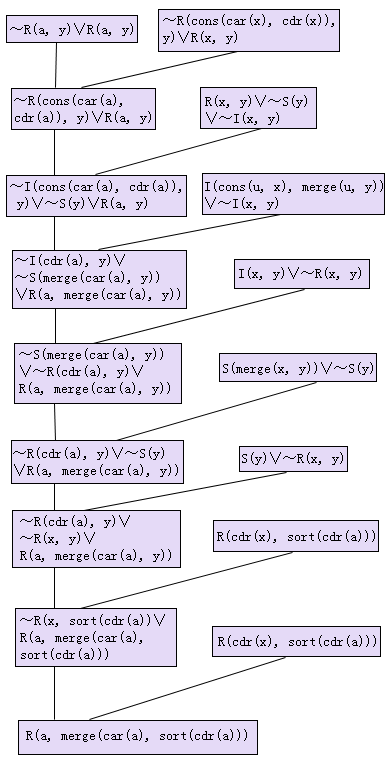
图4.18 x非空时的修改证明树

目标公式为（y）R（nil， y），目标公式否定式~R（nil， y），在这种情况下，归结反演树如图4.17所示，由此可构造出修改证明树，从根部子句得到的回答是R（nil， nil），其意义是若表x的长度为0，则表y的长度也为0。
②x为非空表
作归纳法假设：对任一非空表x，cdr（x）可以排序，即可以认为有某种排序函数"Sort"具有能够实现对小表排序的功能，这样可得归纳假设的子句形
（6）R（cdr（x），Sort（cdr（x）））
现在要证明（x）（y）R（x，y），还要用到一个关系
（x）（cons（car（x）），cdr（x））＝x）
为了避免处理等值谓词带来的复杂性，可引入如下事实：
（x）（y）（R（cons（car（x）， cdr（x））， y）→R（x， y）
因此有
（7）~R（cons（car（x）， cdr（x））， y）∨R（x， y）
目标公式否定式为~R（a， y），其中a是Skolem常量，根据提取回答的过程可得修改证明树如图4.18所示，提取的回答语句为
R（a， merge（car（a）， sort（cdr（a））））
如将Skolem函数用新变量替代，则可改写成
R（x， merge（car（x）， sort（cdr（a））））
将以上两种情况的结果结合起来，最后可得递归程序