4.5 基于归结的自动程序综合

　　自动程序综合是一个困难的研究课题，目前还在发展阶段，本节只是从应用归结法的提取回答过程来讨论自动生成某些简单计算机程序的方法问题。
　　设要生成的程序，输入是x，输出是y，x和y应满足某种特殊关系R（x， y）。假定谓词R的解释适合用某个公理集来定义，而构造程序使用的基本函数的定义则由另一些公理给定.如果某个定理证明系统能证明目标公式（ x）（ y）R（x，y）是公理集的逻辑推论，则在应用提取回答的过程中，这个证明系统就能生成出所要求的程序，即在回答语句中，y将以若干基本函数的组合形式给出，这些函数的组合就是要生成的程序。下面举例说明这种方法的基本思想。
　　设我们要生成一个程序实现数字的排序，该程序的输入是一个数字表x，输出是另一个数字递增的有序表。描述这个程序构造的基本函数可使用LISP语言的系统函数（car、cdr cons等）和自定义的函数（merge），它们的功能定义如下：
car（x）：返回x的第一个元素；
cdr（x）：返回除x中第一个元素以外的剩余表；
cons（e， x）：返回元素e加到表x之前的新表，如
cons（car（x）， cdr（x））＝x；
merge（e， 1）：返回元素e插入已排序表1中组成的一个新的有序表。
现在再引入几个公理，对问题的定义以及输入输出的关系R（x， y）进行形式化描述：
（1）（x）（y）（（R（x， y）→（S（y）∧I（x， y））∧（（S（y）∧I（x， y））→R（x， y）））
其中S（y）表示表y是一个有序表，I（x， y）表示表x和表y元素数目相同但排序不同，I（x， y）和S（y）可根据基本函数递归定义如下：
（2）（x）（y）（u）（I（x， y）→I（cons（u， x）， merge （u， y）））
（3）I（nil， nil），（nil是空表）
（4）（x）（y）（S（y）→S（merge（x， y）））
（5）S（nil）
这些公式经过化简后得子句集：
（1a）~R（x， y）∨S（y）
（1b）~R（x， y）∨I（x， y）
（1c）~S（y）∨I（x， y）∨R（x， y）
（2）~I（x， y）∨I（cons（u， x）， merge（u， y））
（3）I（nil， nil）
（4）~S（y）∨S（merge（x， y））
（5）S（nil）
证明的目标公式：（x）（y）R（x， y）
我们用归纳法来证明这个目标公式，先证明长度n＝0的表，然后假设n≥0成立，证明n+1仍成立。结果得到一个对任意长度的表进行排序的递归函数。
①x的长度n＝0

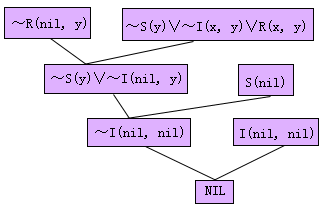
图4.17 n＝0的归结反演树