例4：已知一个公理：P（B，w，w）∨P（A，u，u）
目标公式：（ x）（z）（y）P（x，z，y）
目标否定式： ~P（x，g（x），y）
它含有Skolem函数g（x），如将图4.15反演树中g（x）用新变量t替代，则从修改证明树得到的回答语句为P（A，t，t）∨P（B，z，z）。
前面介绍归结方法时曾经说过，当一个子句在归结中多次使用时，可以对变量进行换名。在该例的修改证明树中，当第二次使用子句～P(x, t, y)∨P(x, t, y)进行归结时，由于两个归结式中均有变量t，为了区分他们是两个不同的变量，用变量z代替了变量t。
例5：已知一个公量：P（z，u，z）∨P（A，u，u）
目标公式：（ x）（z）（y）P（x，z，y）
目标否定式： ~P（x，g（x），y）

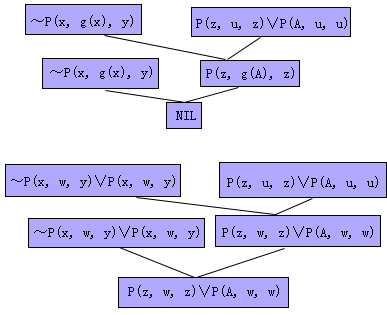
图4.16 例5反演树和修改证明树

　　该例中用w代替Skolem函数g（x），得到的反演树和修改证明树如图4.16所示，可得回答语句P（z， w， z）∨P（A， w， w）从这个例子看出，归结过程两棵树对应的合一集是相同的，但修改证明树中所用的置换更一般些。
通过以上几个例子，可归纳出提取回答过程中的步骤如下：
（1）使用某种搜索策略求出一个归结反演树，树中对合一集加一标记；
（2）目标公式否定式化简得到的子句中，对出现的任一Skolem函数均以新变量置换；
（3）根据目标公式否定式的子句，构造重言式；
（4）按照已找到的归结反演树的结构，将目标否定式子句用永真式替代，且每次归结合一文字集不变，生成出修改证明树；
（5）根部子句就作为所要提取的回答语句。
　　由这个过程所得到回答语句显然取决于归结反演树，因为对同一问题可能存在若干个不同的反演证明过程。这样每一个反演都可提取一个回答，而所有的回答语句中，有的可能相同，但总可能有较一般的回答语句。由于谓词演算的不可判定性，我们无法判定所提取的回答是否最一般的回答。