（3）目标公式含有全称量词量化变量的情况
　　在这种情况下，目标否定式出现存在量词，因而化简后目标否定式有Skolem函数，我们用下面的例子来说明这种情况下的处理办法。
例3：已知For all x， x is the child of p（x）. For all x and y， if x is the child of y， then y is the parent of x.
询问：For any x ， who is the parent of x?
事实公式集：
（x）C（x，p（x））
（x）（y）（C（x，y）→P（y，x））
目标公式：（x）（y）P（y，x）
基本子句集S为
{C（x1，P（x1）），~C（x2，y1）∨P（y1，x2），~P（y2，A）}
　　这个例子很简单，得到的修改证明树如图4.14所示，回答语句是P（P（A），A），其中A是化简目标否定式消去存在量词时引进的Skolem函数（常量）。可以证明在回答提取过程中，可以用一个新变量取代目标否定式子句中任一Skolem函数是正确的，这些新变量经过替换过程仍会出现在回答的语句中，下面再举两个例子说明这个替换过程。

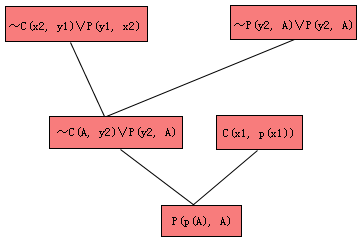
图4.14例3的修改证明树

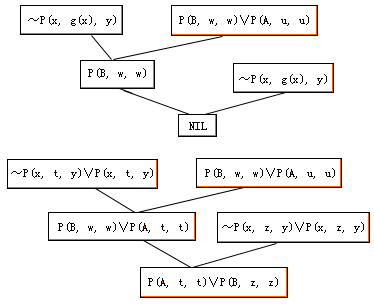
图4.15 例4反演树和修改证明树